Similitudes Lineal-Rotacional

| Mas comparaciones entre movimientos lineal y angular |
Conceptos sobre Momento de Inercia
| HyperPhysics*****Mecánica*****Rotación | M Olmo R Nave |
Similitudes Lineal-Rotacional
|
Indice Conceptos sobre Momento de Inercia | ||
|
Atrás |
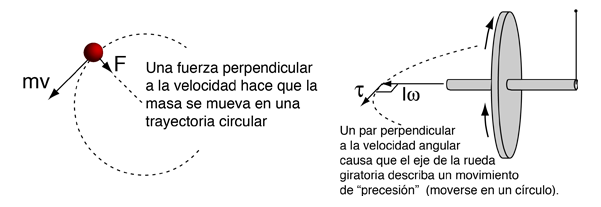
Similitudes Lineal-Rotacional
|
Indice Conceptos sobre Momento de Inercia | ||||
|
Atrás |
Momento de InerciaMomento de inercia es el nombre que se le da a la inercia rotacional. En la tabla de arriba se ve que su análogo en el movimiento lineal es la masa. Aparece en las relaciones de la dinámica del movimiento rotacional. El momento de inercia debe especificarse respecto a un eje de rotación dado. Para una masa puntual el momento de inercia es exactamente el producto de la masa por el cuadrado de la distancia perpendicular al eje de rotación, I = mr2. Esa relación de la masa puntual, viene a ser la base para todos los demás momentos de inercia, puesto que un objeto se puede construir a partir de una colección de puntos materiales. 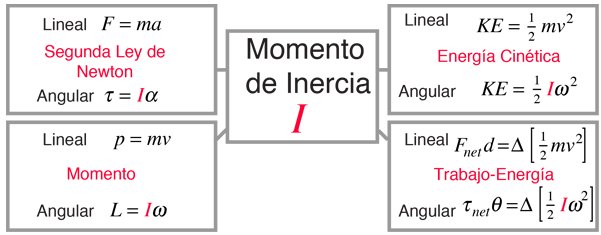
|
Indice Conceptos sobre Momento de Inercia | ||||
|
Atrás |
Momentos comunes de inercia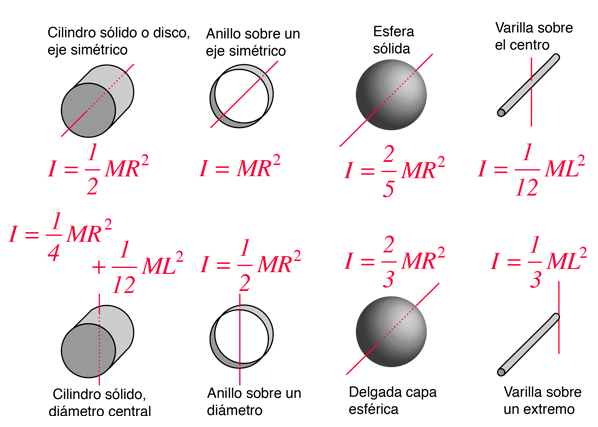 |
Indice Conceptos sobre Momento de Inercia | ||
|
Atrás |
Ejemplos de momentos de inerciaEl momento de inercia se define con respecto a un determinado eje de rotación. El momento de inercia de una masa puntual con respecto a un eje se define como el producto de la masa por la distancia perpendicular al eje elevada al cuadrado. El momento de inercia de cualquier objeto extenso, se construye a partir de esa definición básica. La forma general del momento de inercia involucra una integral. 
|
Indice Conceptos sobre Momento de Inercia | ||
|
Atrás |
Momento de Inercia. Forma GeneralPuesto que el momento de inercia de un objeto ordinario involucra una continua distribución de masa a una distancia continuamente variable de cualquier eje de rotación, el cálculo del momento de inercia, generalmente involucra el cálculo diferencial, la disciplina de las matemáticas que puede manejar tales variables continuas. Puesto que el momento de inercia de una masa puntual se define por  entonces, la contribución al momento de inercia por un elemento de masa infinitesimal dm tiene la misma forma. A esta clase de elemento de masa se le llama un elemento diferencial de masa y su momento de inercia está dado por  Note que el elemento diferencial del momento de inercia dI debe estar siempre definido con respecto a un específico eje de rotación. La suma sobre todos estos elementos se llama integral sobre la masa. 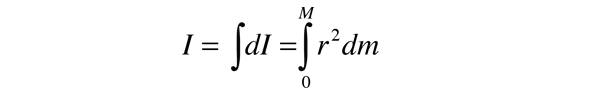 Usualmente, el elemento de masa dm será expresado en términos de la geometría del objeto, de modo que la integración puede llevarse a cabo sobre el objeto como una totalidad (por ejemplo, sobre una varilla larga uniforme). Habiendo llamado esto una forma general, es probablemente apropiado señalar que es una forma general solamente para ejes llamados "ejes principales", un término que incluye todos los ejes de simetría del objeto. El concepto de momento de inercia para objetos en general sobre ejes arbitrarios es un asunto mucho mas complicado. En tales casos el momento de inercia toma la forma de una cantidad de tensor matemático que requiere nueve componentes para definirlo completamente.
|
Indice Conceptos sobre Momento de Inercia | ||||
|
Atrás |