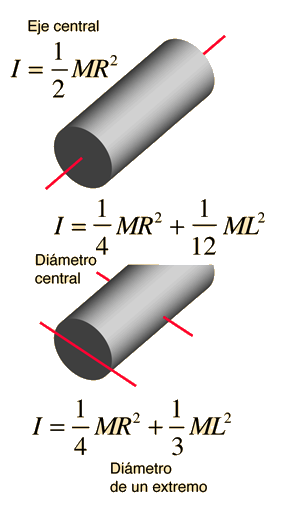
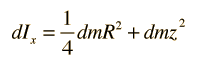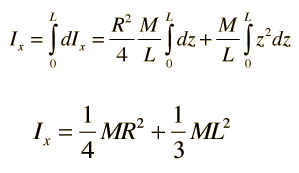Momento de Inercia: Cilindro sobre Eje Perpendicular
El desarrollo de la expresión del momento de inercia de un cilindro sobre el diámetro de un extremo (el eje x en el diagrama), hace uso de ambos, el teorema de ejes paralelos y el teorema de ejes perpendiculares. El enfoque consiste en encontrar una expresión para un disco delgado a una distancia z del eje, y hacer la suma de todos esos discos
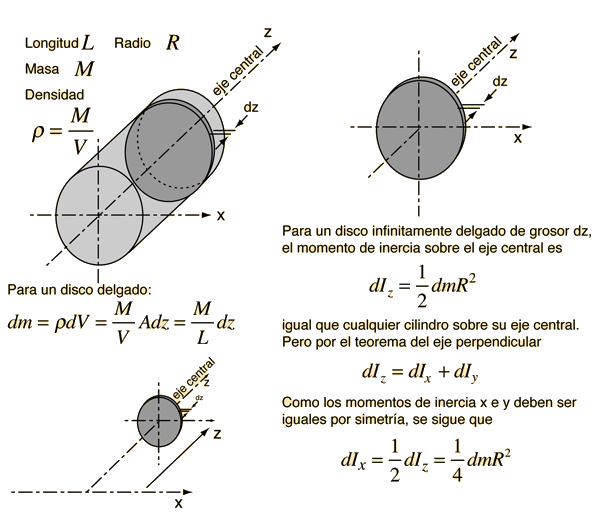
La obtención del momento de inercia de un cilindro completo sobre un diámetro de su extremo, consiste en una suma de infinitos discos delgados, a diferentes distancias de ese eje. Esto nos lleva a una integral desde z=0 hasta z=L. Para cualquier disco dado a una distancia z de su eje x, usando el teorema de los ejes paralelos, nos da el momento de inercia sobre el eje x.
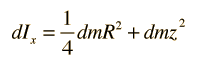
Ahora, expresando el elemento de masa dm en términos de z, podemos integrar sobre la longitud L del cilindro.
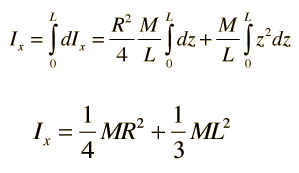
Esta fórmula se puede ver que es plausible si tiene en cuenta, que es la suma de la expresión para un disco delgado sobre un diámetro, mas la expresión para una varilla delgada sobre su extremo. Si toma el caso límite de R=0, obtiene la expresión de la varilla delgado y si toma el caso límite de L=0, obtiene la expresión del disco delgado.
Los últimos pasos hacen uso de la forma polinómica de las integrales.
|