Límites

La mayoría de las aplicaciones del cálculo tratan con funciones continuas, pero la visualización del proceso, a menudo comienza con cambios finitos en la variable de interés. Una de las potencias del cálculo es el de tratar con cambios que son infinitesimalmente pequeños. Por ejemplo, la velocidad promedio se obtiene tomando la distancia recorrida, y dividiéndola por el intervalo de tiempo finito que llevó recorrer esa distancia. Pero supongamos que queremos la velocidad instantánea en un determinado instante del tiempo. Podemos aproximarnos a ello con un "límite", es decir, podemos tomar las distancias mas cortas recorridas en los intervalos mas cortos, y dividiéndola por esos tiempos mas cortos. Si a este proceso se le permite continuar hasta que los intervalos de tiempo se acercan a cero, entonces estamos haciendo lo que llamamos "tomando el límite cuando el tiempo tiende a cero". Esta es la forma en que definimos una derivada de la distancia respecto al tiempo, y la forma de obtener la velocidad instantánea, usando los métodos del cálculo. Los límites también se usan para la formación de las integrales, o anti-derivadas. 		Índice
 
HyperPhysics*****HyperMath*****CálculoM Olmo R Nave
 Atrás





Forma Diferencial

Como paso previo para llevar a cabo las operaciones del cálculo tales como las derivadas y las integrales, la expresión matemática debe colocarse en forma diferencial, para aplicarle los métodos de variables continuas. Por ejemplo, en el desarrollo de la fórmula del decaimiento radioactivo tenemos la expresión de diferencia finita:

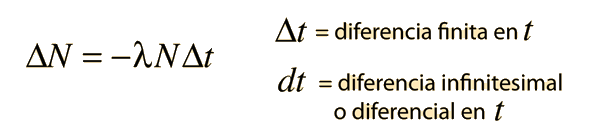
Es una práctica estándar usar la letra griega Δ para representar una diferencia finita. A menudo, las fórmulas de diferencias finitas son solo aproximadamente verdad y son exactamente verdad solamente en el límite, donde las diferencias vienen a ser infinitesimalmente pequeñas. En este límite, el intervalo de tiempo Δt viene a ser practicamente cero, y como resultado, el número de decaimientos N también viene a ser practicamente cero. La letra Δ se reemplaza por el símbolo diferencial d y la forma resultante

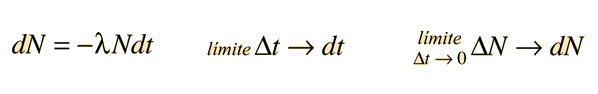
se dice que es la forma diferencial de la expresión.

Aplicación al Decaimiento Radioactivo
 Índice
 
HyperPhysics*****HyperMath*****CálculoM Olmo R Nave
 Atrás