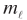Momento Angular en un Campo Magnético
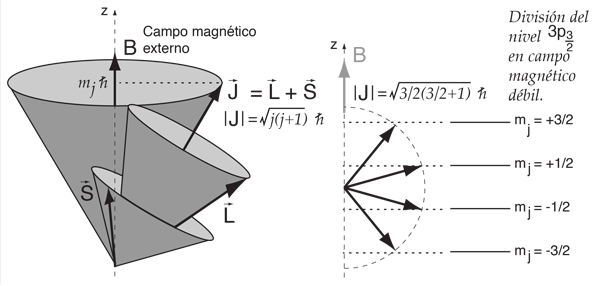
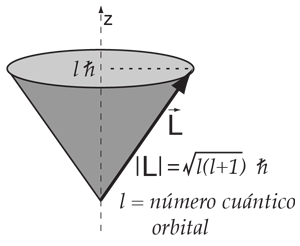
Una vez que se han combinado el momento angular orbital y de espín de acuerdo con el modelo vectorial, el momento angular total resultante, se puede visualizar como precesión alrededor de cualquier campo magnético aplicado externamente.
Este es un modelo útil para tratar con interacciones, tales como el efecto Zeeman en el sodio. La contribución de energía magnética es proporcional a la componente del momento angular total sobre la dirección del campo magnético, que se define generalmente como dirección z.
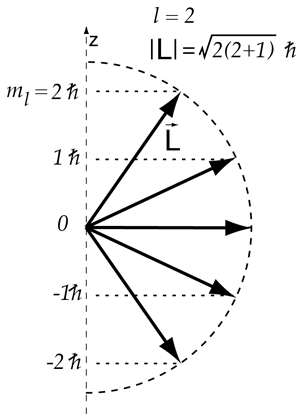
La componente z del momento angular está cuantizada en valores que difieren una unidad, por lo que para el nivel superior del doblete de sodio con j=3/2, el modelo vectorial da el desdoblmiento que se muestra.
Incluso con el modelo vectorial, la determinación de la magnitud del desdoblamiento Zeeman no es trivial, ya que las direcciones de S y L estan cambiando constantemente a medida que precede sobre J. Este problema se resuelve con el factor g de Lande.
Este tratamiento del momento angular es apropiado para débiles campos magnéticos externos, donde se presume que el acoplamiento entre el momento angular orbital y de espín, es mas fuerte que el del campo magnético externo. Esto puede ser visualizado con la ayuda de un modelo vectorial del momento angular total. Si el campo externo es muy fuerte, entonces puede desacoplar el momento angular orbital y el de espín. Este caso de campo fuerte, se llama efecto Paschen-Back, y da lugar a diferentes patrones de desdoblamientos de los niveles de energía.
|