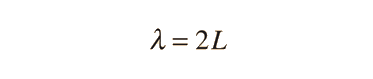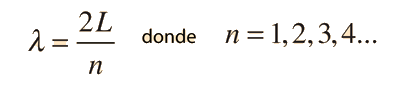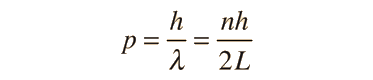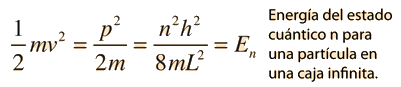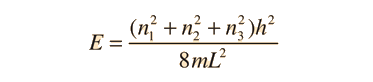La Ecuación de Schrodinger

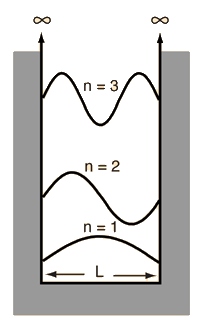
La ecuación de Schrödinger desempeña el papel de las leyes de Newton y la conservación de la energía de la mecánica clásica, -es decir, predice el comportamiento futuro de un sistema dinámico-. Se trata de una ecuación de onda en términos de la función de onda, que predice analíticamente y con precisión, la probabilidad de eventos o resultados. El resultado detallado no está estrictamente determinado, pero dado un gran número de eventos, la ecuación de Schrodinger predice la distribución de los resultados.

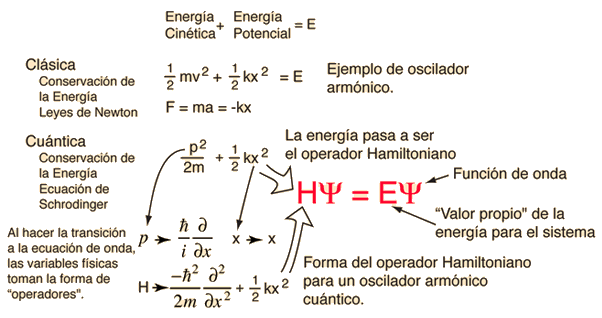
Las energías cinética y potencial se transforma en el hamiltoniano que actúa sobre la función de onda, para generar la evolución de la función de onda en el tiempo y el espacio. La ecuación de Schrödinger da las energías cuantizadas del sistema, y da la forma de la función de onda, de manera que pueden ser calculadas otras propiedades.

Partícula en una Caja

La situación idealizada de una partícula en una caja con paredes infinitamente altas, es una aplicación de la ecuación de Schrodinger, que da algunas ideas sobre el confinamiento de partículas. La función de onda debe ser cero en las paredes y la solución de la función de onda produce sólo ondas sinusoidales. La mayor longitud de onda es y los modos superiores tienen longitudes de onda dadas por Cuando esto se sustituye en la relación de DeBroglie, produce el momento

Partícula en una Caja

Calcular

Cuando se usa la expresión del momento de la partícula en una caja : para calcular la energía asociada con la partícula Aunque simplista, esto indica algunas cosas importantes sobre los estados ligados de partículas: 1. Las energías están cuantizadas y pueden ser caracterizadas por un número cuántico n. 2. La energía no puede ser exactamente cero. 3. Cuanto menor es el confinamiento, más grande es la energía necesaria. Si una partícula está confinada en un volumen rectangular, el mismo tipo de proceso se puede aplicar a una "partícula en una caja" de tres dimensiones, y se hace el mismo tipo de aportación de energía desde cada dimensión. Las energías para una caja tridimensional son Esto da una expresión física más realista de las energías disponibles en las partículas contenidas. Esta expresión se utiliza, en la determinación de la densidad de estados de energía posibles, para los electrones en los sólidos.

Cálculo de Partícula en una Caja

A continuación se puede calcular la energía de partícula en una caja de una dimensión. Para una caja tridimensional habrá tres valores de número cuántico n. Se pueden calcular las energías para cada dimensión y sumarse. La implicación de esa suma es, que se necesita más energía para confinar una partícula en tres dimensiones, que en una, y que la energía mínima de confinamiento para una caja de 3D de dimensión L, es tres veces el de una caja de 1D.

L = x 10^ m = a₀ = fermi* = radio de protón**,

y masa = x 10^ kg = m_e = m_p = MeV/c²,

entonces, la energía para el estado n = para una caja de una-dimensión es

E = x 10^julios = eV = MeV = GeV.

Se puede obtener el estado fundamental de una caja tridimensional de dimensión L, estableciendo n=1 para las tres dimensiones, dando una energía tres veces la energía del estado fundamental de la caja unidimensional. El estado fundamental para la caja tridimensional sería E3D ground = x 10^julios = eV = MeV = GeV. * 1 fermi = 10-15m. ** El radio clásico del protón se ha calculado tomando la densidad nuclear nominal de 2,3x1017 kg/m3. Nota: Si se cambia el valor de la energía, entonces el estado se establece a n=1 y se calcula la dimensión L de la caja. Cualquier otro cambia inicia un nuevo cálculo de la energía.

Comparar con el Principio de Incertidumbre

Energías en eV

Caja de Pared Finita

Ejemplo de Energía Necesaria para Confinar Partículas