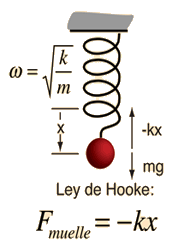
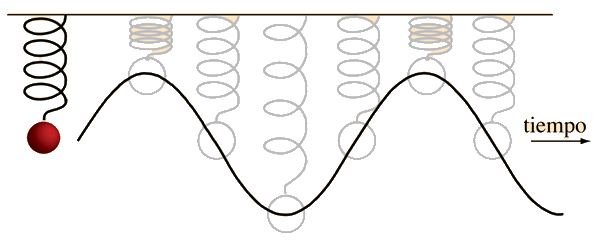
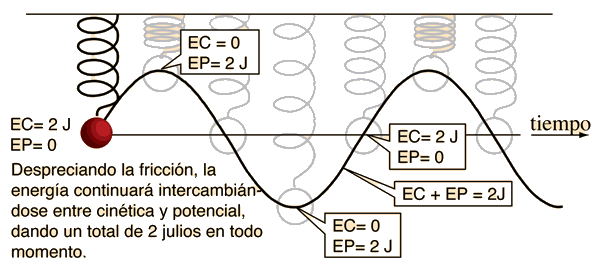
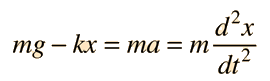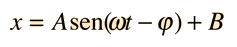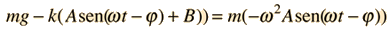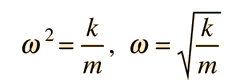Frecuencia del Movimiento Armónico Simple

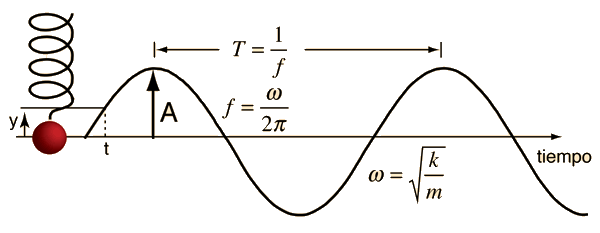
La frecuencia del movimiento armónico simple como en una masa sobre un muelle, se determina por la masa m y la rigidez del muelle, expresado en términos de la constante de elasticidad del muelle k ( ver ley de Hooke):

Resonancia de Masa sobre Muelle

Una masa sobre un muelle, tiene una simple frecuencia de resonancia, determinada por su constante de elasticidad k y la masa m. Usando la ley de Hooke y despreciando la amortiguación y la masa propia del muelle, la segunda ley de Newton, da la ecuación del movimiento: La solución de esta ecuación diferencial es de la forma: que cuando se sustituye en la ecuación del movimiento, da: Agrupando términos da B=mg/k, que es exactamente el alargamiento del muelle por el peso y la expresión para la frecuencia de vibración de resonancia será : A esta clase de movimiento se le denomina movimiento armónico simple, y al sistema, oscilador armónico simple.

Masa sobre Muelle: Secuencia del Movimiento

Una masa sobre un muelle, trazará un patrón sinusoidal como función del tiempo, como cualquier objeto que vibra en un movimiento armónico simple. Una forma de visualizar este patrón es caminar en línea recta a velocidad constante, mientras lleva consigo la masa vibrando. Entonces la masa trazará un camino sinusoidal en el espacio y en el tiempo.

Mostrar la Transformación de Energía que Participa en este Movimiento.

Energía en Masa sobre Muelle

El movimiento armónico simple de una masa sobre muelle, es un ejemplo de una transformación de energía entre energía potencial y energía cinética. En el ejemplo de abajo, se asume que se ha efectuado un trabajo de 2 julios, para poner la masa en movimiento.