El Principio de Incertidumbre

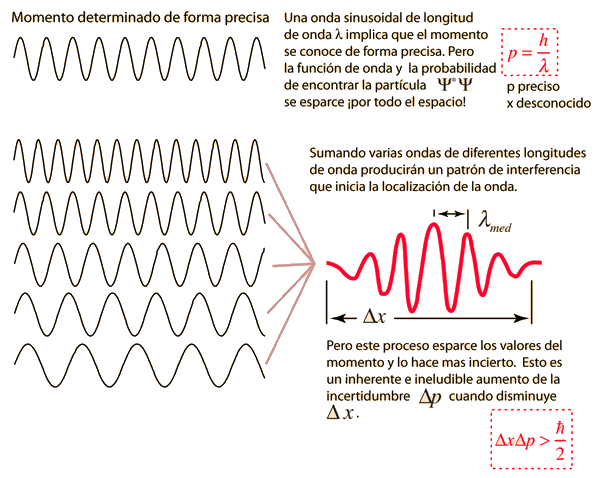
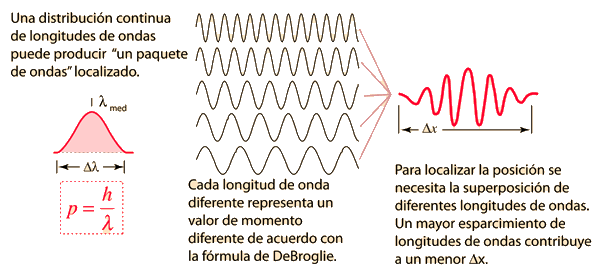
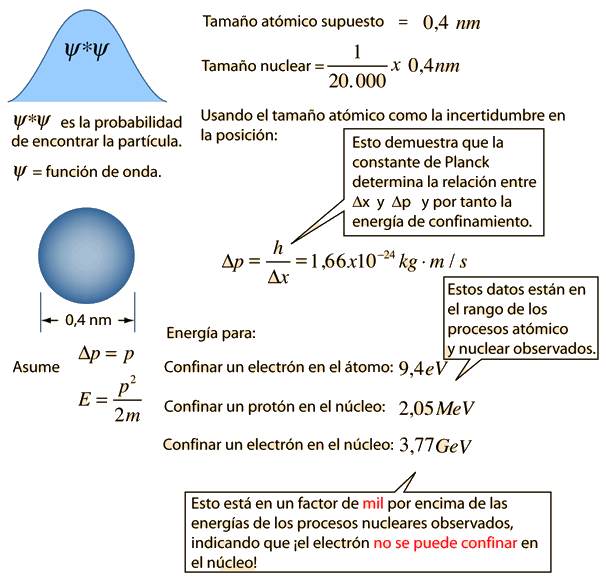
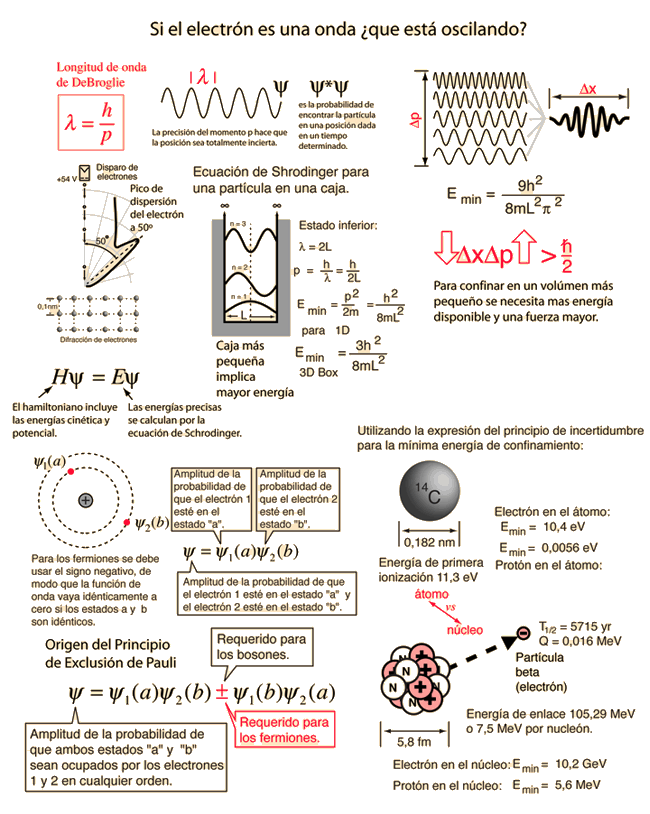
La posición y el momento de una partícula, no se pueden medir simultáneamente con una precisión arbitrariamente alta. El producto de las incertidumbres de estas dos mediciones tiene un mínimo. Igualmente, existe un mínimo para el producto de las incertidumbres de la energía y el tiempo.

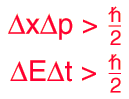
Esto no es una declaración sobre la inexactitud de los instrumentos de medida, ni una reflexión sobre la calidad de los métodos experimentales, sino que surge de las propiedades de onda inherentes, en la descripción de la naturaleza de la mecánica cuántica. Incluso con instrumentos y técnica perfectas, la incertidumbre es inherente con la naturaleza de las cosas.

Principio de Incertidumbre

Los pasos importantes en el camino hacia la comprensión del principio de incertidumbre son, la dualidad onda-partícula y la hipótesis de DeBroglie. A medida que se avanza hacia abajo en tamaño, hacia las dimensiones atómicas, ya no es válido considerar la partícula como una esfera sólida, porque cuanto menor es la dimensión, más se vuelve en forma de onda. Ya no tiene sentido decir que se ha determinado con precisión la posición y el momento de una partícula. Cuando se dice que el electrón actúa como una onda, entonces la onda es la función de onda de la mecánica cuántica y por lo tanto, se relaciona con la probabilidad de encontrar el electrón en cualquier punto del espacio. Una sinusoide perfecta para la onda del electrón, propaga esa probabilidad a lo largo de todo el espacio, y entonces, la "posición" del electrón es completamente incierta.

Confinamiento de una Partícula

El principio de incertidumbre contiene implicaciones sobre la energía que se requeriría, para contener una partícula dentro de un volumen dado. Esta energía necesaria para contener la partícula proviene de las fuerzas fundamentales. En particular, la fuerza electromagnética proporciona la atracción necesaria para contener los electrones dentro del átomo, y la fuerza nuclear fuerte, proporciona la atracción necesaria para contener las partículas dentro del núcleo. Pero la constante de Planck que aparece en el principio de incertidumbre, determina el tamaño del confinamiento que puede ser producido por estas fuerzas. Otra forma de decirlo es, que las intensidades de las fuerzas nucleares y electromagnéticas, junto con la limitación incorporada en el valor de la constante de Planck, determinan las escalas del átomo y el núcleo.

El siguiente cálculo muy aproximado, sirve para dar el orden de la magnitud de las energías necesarias para contener las partículas.

Cálculo del Confinamiento

Si se examina este cálculo en detalle, se dará cuenta de que se realizó una aproximación bruta en la relación Δp = h/Δx. Esto se hizo para obtener una relación cualitativa que muestre el papel de la constante de Planck en la relación entre Δx e Δp, y por lo tanto el papel de h en la determinación de la energía de confinamiento. La otra razón para hacerlo era conseguir una energía de confinamiento de electrones, próxima a la que se observa en la naturaleza, para la comparación con la energía de confinamiento de un electrón en el núcleo. Si se utiliza realmente el caso límite permitido por el principio de incertidumbre, Δp = hbar/2Δx, la energía de confinamiento que se obtiene para el electrón en el átomo, es sólo 0,06 eV. Esto se debe a que este enfoque sólo confina el electrón en una dimensión, dejándolo sin confinar en las otras direcciones. Para un átomo más realista se tendría que encerrarlo también en las otras direcciones. Se puede obtener una mejor aproximación desde el enfoque de una partícula en una caja en 3-D, pero para calcular con precisión la energía de confinamiento, se requiere la ecuación de Shrodinger (ver cálculo del átomo de hidrógeno).

Contexto de la Función de Onda