Oscilador Armónico Cuántico
Una molécula diatómica vibra algo así como dos masas sobre un muelle, con una energía potencial que depende del cuadrado del desplazamiento desde la posición de equilibrio. Sin embargo, los niveles de energía están cuantizados en valores igualmente espaciados.
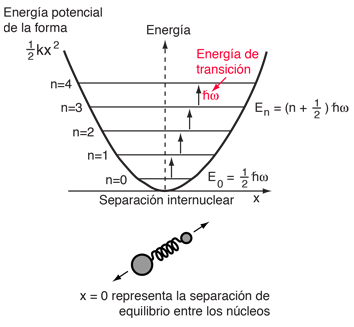 |
Los niveles de energía del oscilador armónico cuántico son  y para una molécula diatómica, la frecuencia natural es de la forma  donde la masa reducida esta dada por 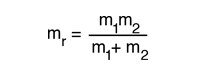 |
Esta forma de la frecuencia es la misma que la del oscilador armónico simple clásico. La diferencia más sorprendente para el caso cuántico, es la llamada vibración del punto-cero" del estado fundamental n=0. Esto implica que las moléculas no están completamente en reposo, incluso a la temperatura del cero absoluto.
El oscilador armónico cuántico tiene implicaciones más allá de la simple molécula diatómica. Es la base para la comprensión de los modos complejos de vibración en las moléculas más grandes, el movimiento de los átomos en una red sólida, la teoría de la capacidad calorífica, etc. En los sistemas reales, los espaciamientos de energía son solamente iguales en los niveles mas bajos, donde el potencial es una buena aproximación al potencial armónico del tipo de "masa sobre un muelle". Los términos inarmónicos que aparecen en el potencial de una molécula diatómica, son útiles para mapear el potencial detallado de tales sistemas.
| Ecuación de Schrodinger para el Oscilador Armónico | Funciones de Onda |
| Principio de Correspondencia | Distribuciones de Probabilidad |
Conceptos de la Ecuación de Schrödinger
Referencias
Beiser, Perspectives
Sec 8-7
Blatt
Sec 7-9
| HyperPhysics*****Física Cuántica | M Olmo R Nave |