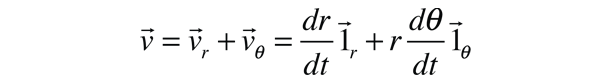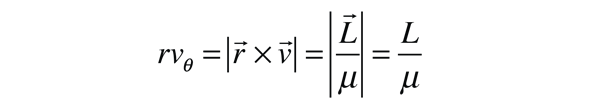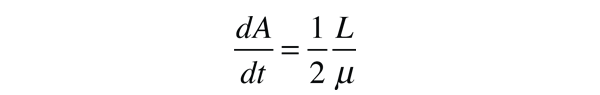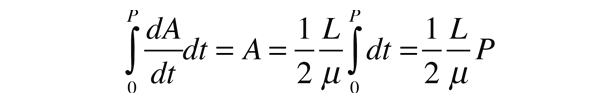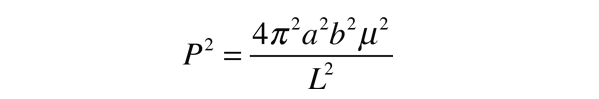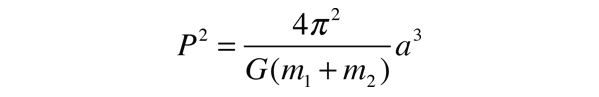Desarrollo de la Ley de las Órbitas de Kepler
Ley de las Órbitas: dos masas orbitándose entre sí por órbitas entrelazadas bajo la influencia de la ley de la gravedad describirán órbitas elípticas alrededor del centro de masa del sistema de ambos cuerpos.
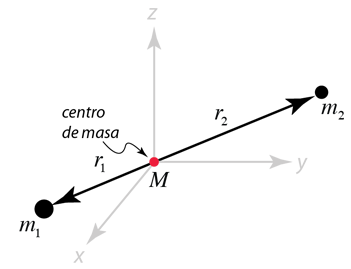 | El movimiento de un sistema binario puede describirse en relación con el centro de masa del sistema. La distancia del vector entre las dos masas es 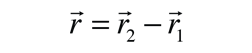 y el movimiento de una de las masas con relación a la otra usa el concepto de masa reducida : 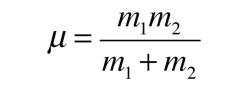 |
Las coordenadas vectoriales individuales de las masas pueden expresarse en términos de la masa reducida:

Las leyes de Kepler dependen del principio de conservación del momento angular, y como éstas son inherentemente cantidades vectoriales, el momento angular se expresa en términos de productos vectoriales. El momento angular de un sistema de dos cuerpos puede expresarse en términos de su velocidad relativa y de la masa reducida del sistema. Comenzando con los momentos angulares individuales, el momento angular del sistema L puede expresarse como sigue:
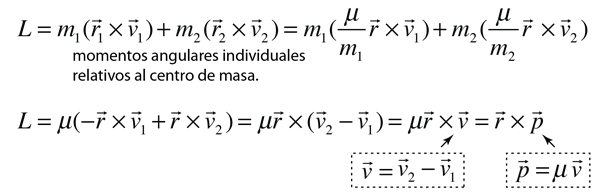
Esto proporciona el marco de trabajo necesario para demostrar que el momento angular se conserva para un planeta en órbita o para un miembro de un sistema estelar binario. Esto se hace mostrando que la derivada del momento angular es cero para el caso en que la fuerza de atracción actúa a lo largo de la línea entre los dos cuerpos. Esto requiere la expresión de la derivada de un producto de funciones. Utilizando la expresión para el momento angular L obtenido anteriormente:
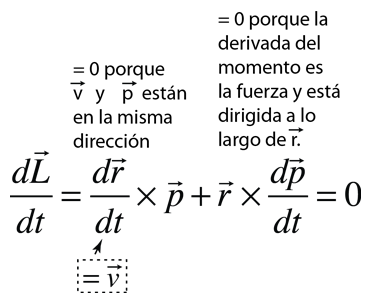 | Esto establece el hecho de que el momento angular L se conserva para cualquier sistema de dos masas orbitales sometidas a una fuerza central. La conservación del momento angular conduce tanto a la Ley de Órbita de Kepler como a la Ley de Áreas. |
La órbita de una de las masas en un sistema binario puede ser descrita como el movimiento de la masa reducida alrededor de un punto a la distancia relativa r donde se coloca la masa total. La magnitud de r es la misma que la distancia relativa r en el desarrollo anterior | 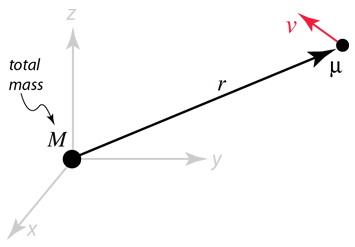 |
La determinación de que el movimiento de ambas masas en un sistema binario ejecute órbitas elípticas alrededor de un punto focal en el centro de masa del sistema, requiere el análisis de la fuerza y el momento angular del sistema. El momento angular L del sistema puede expresarse como
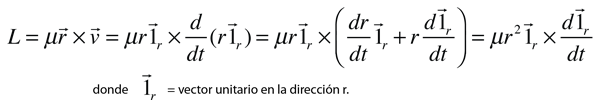
En esta expresión, se han introducido los vectores unitarios en la dirección r debido a que tanto la magnitud de r como su dirección pueden cambiar. Obsérvese que un término cae fuera de la expresión del producto vectorial porque contiene el producto vectorial del vector unitario por sí mismo y es por tanto cero.
La aceleración de la masa reducida esta dada por
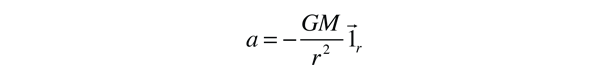
donde M es la masa total del sistema. Como estrategia para obtener la expresión para r, se hace la siguiente evaluación:
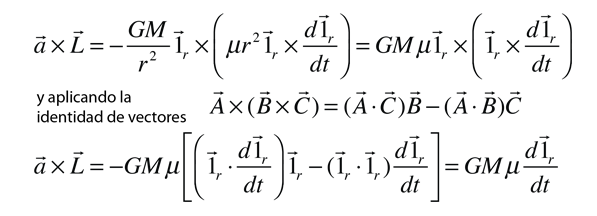
Donde se utilizan además de la identidad vectorial, los hechos de que el producto escalar de dos vectores unitarios es igual a 1 y el producto escalar del vector unitario por su derivada es igual a 0,.
Siguiendo una estrategia dirigida a encontrar una expresión para el radio vector r en términos del momento angular, la expresión anterior se modifica de modo que sea una igualdad de dos derivadas. Se usa la regla para la derivación de un producto junto con el hecho de que dL/dt=0 (conservación del momento angular).
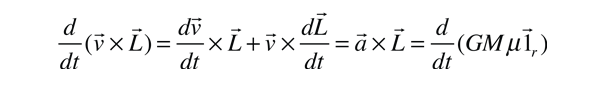
Ahora la integración de las dos cantidades diferenciales da
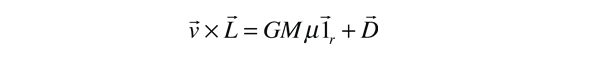
Donde podemos sostener que la constantede de integración vectorial D debe estar en el plano de la órbita, ya que las otras dos cantidades están en ese plano. Para introducir el radiovector r en esta expresión se sigue el siguiente procedimiento con la identidad vectorial.
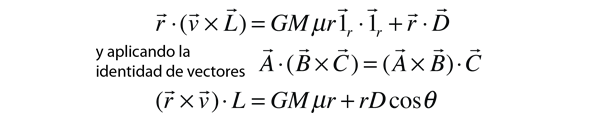
Usando la expresión final para el momento angular L de arriba, esto puede ser puesto en la forma
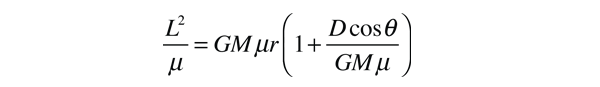
El paso final para mostrar que esta es la expresión de una órbita de sección cónica es definir e=D/GMμ de modo que el radio r se convierte en
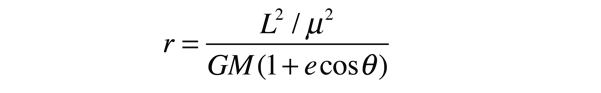
Esta forma para la ecuación de una sección cónica se expresa en términos del momento angular L, la excentricidad e, y el ángulo θ medido desde el perihelio. For e<1 esto es la forma de una elipse y se puede expresar en términos del semieje mayor a.
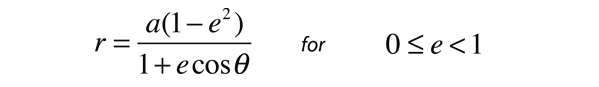
Estableciendo estas dos expresiones iguales entre sí da una expresión para el momento angular L

 | Para una órbita binaria entrelazada, cada objeto seguirá una órbita elíptica alrededor del centro de masa del sistema. El centro de masa estará en un foco de cada elipse. |
Conceptos de gravedad
Conceptos de Órbitas
Carroll & Ostlie
Sec 2.3
| HyperPhysics*****Mecánica | M Olmo R Nave |