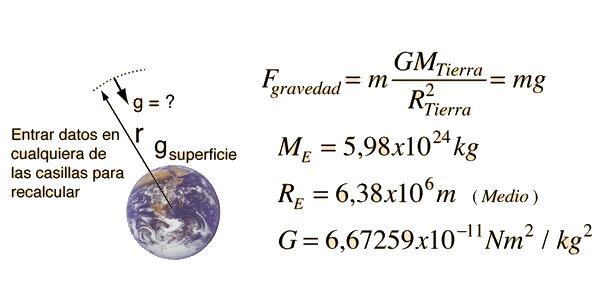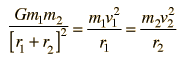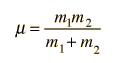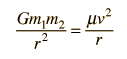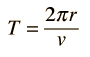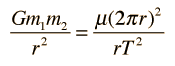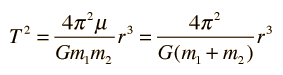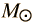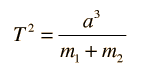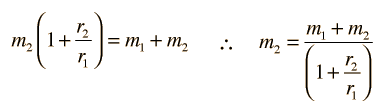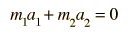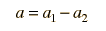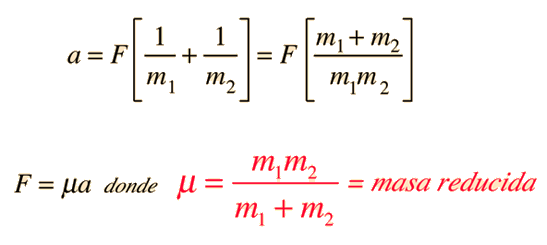Órbita Circular

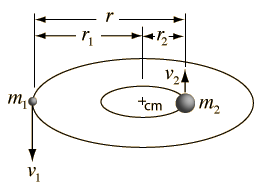
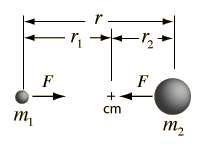
La Gravedad proporciona la fuerza centrípeta necesaria para mantener un satélite en órbita alrededor de la Tierra. La órbita circular es un caso especial, ya que las órbitas son generalmente elipses, o hipérbolas en el caso de objetos que no son más que desviados por la gravedad del planeta, pero no capturados. Estableciendo la fuerza de la gravedad de la ley de gravitación universal, igual a la fuerza centrípeta de un camino curvo, nos conduce a la descripción de la órbita. La órbita se puede expresar en términos de la aceleración de la gravedad en la órbita.

La fuerza de gravedad para mantener un objeto en movimiento circular es un ejemplo de la fuerza centrípeta. La gravedad no realiza trabajo sobre el objeto orbitando en una órbita circular, puesto que siempre actua perpendicular al movimiento.

Gravedad de la Tierra

El peso de un objeto, dado por W=mg, es la fuerza de la gravedad, la cual viene de la ley de gravitación en la superficie de la Tierra en la forma de la ley del inverso del cuadrado:

Al nivel estándar del mar, la aceleración de la gravedad tiene el valor de g = 9.8 m/s², pero este valor disminuye de acuerdo con la ley del inverso del cuadrado a mayores distancias de la Tierra. El valor de g a cualquier altura determinada, digamos la altura de una órbita, se puede calcular de la expresión de arriba.

Tenga en cuenta que el cálculo anterior, da el valor correcto de la aceleración de la gravedad, sólo para valores positivos de h, es decir, los puntos fuera de la Tierra. Si hiciera un agujero hasta el centro de la Tierra, la aceleración de la gravedad se reduciría con el radio, en el camino hacia el centro de la Tierra. Si la Tierra fuera de una densidad uniforme (¡que no lo es!), la aceleración de la gravedad disminuiría de forma lineal hasta la mitad de su valor en la superficie, a la mitad del radio de la Tierra y se aproximaría a cero a medida que se acercara uno al centro de la Tierra.

Órbita Circular Binaria

De la fuerza de la gravedad y la fuerza centrípeta necesaria: Si usted está montando en una de las masas, la ecuación de movimiento relativo tiene la misma forma si sustituye la masa reducida lo cual da la ecuación de la órbita:

Esto nos conduce a la tercera ley de Kepler (la ley de las periodos), la cual es útil para las órbitas de las Lunas y las estrellas binarias.

Puesto que el periodo T de una órbita está dado por

Si usamos las unidades astronómicas convenientes

• r = a en AU (unidades astronómicas en ingles)
• G = 4π²

  m in

  (masas solares)

• T en años

Esto aplica a las órbitas circulares donde a es el radio, y a las órbitas elípticas donde a es el semieje mayor.

Masa Reducida

El movimiento relativo de dos objetos que son afectados por una fuerza central puede ser descrito por la segunda ley de Newton como si fueran masas simples de un valor llamado "masa reducida".

De la tercera ley de Newton :

La aceleración relativa de las dos masas es

Puesto que a₂ es negativa, esto puede reescribirse en términos de magnitudes de las cantidades: