Secciones Cónicas
Las curvas que se obtienen al cortar un cono, se llaman secciones cónicas y tienen muchas aplicaciones. Haga clic en una de ellas para obtener más detalles.
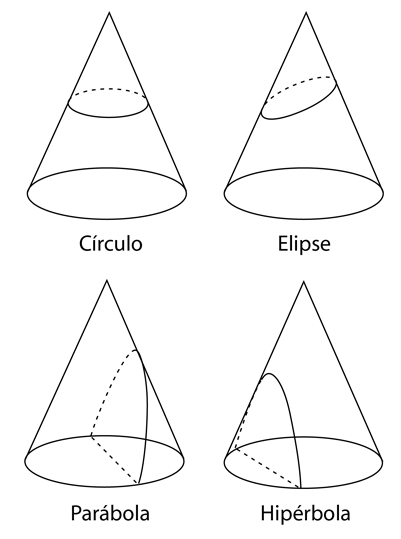
| Una de las aplicaciones es que, una partícula que se mueve y se somete a una fuerza del tipo de la ley del inverso del cuadrado como la gravedad o la ley de Coulomb, seguirá una trayectoria descrita por una de las secciones cónicas. |
Cada una de las secciones cónicas se puede describir en función del semieje mayor a y la excentricidad e. A la derecha se muestran valores representativos de estos parámetros, junto con los tipos de órbitas asociadas con ellos. | 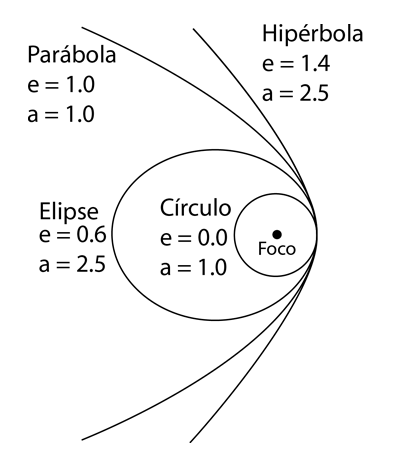 |
Cada ecuación de la forma
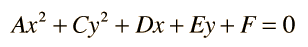
| HyperPhysics*****HyperMath*****Geometría | M Olmo R Nave |