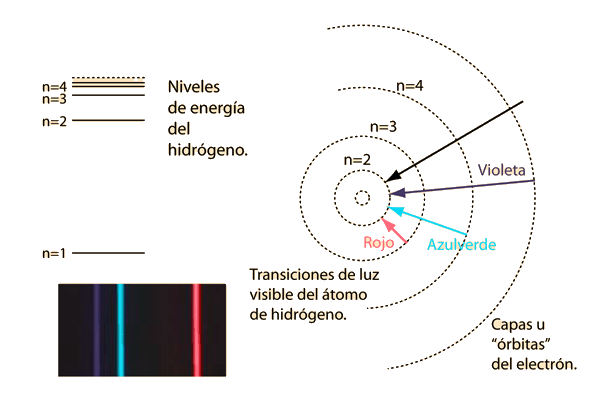
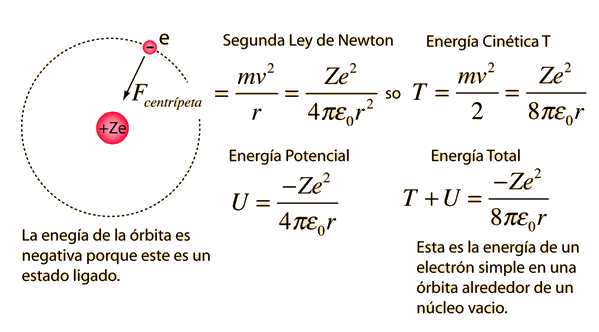
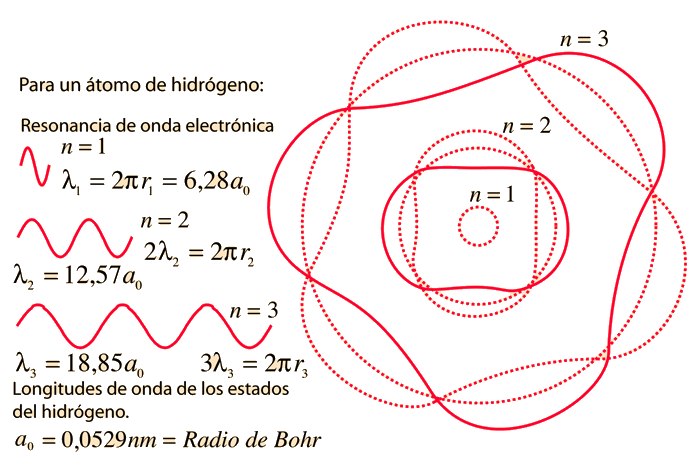
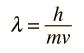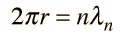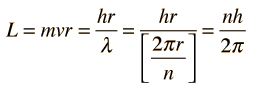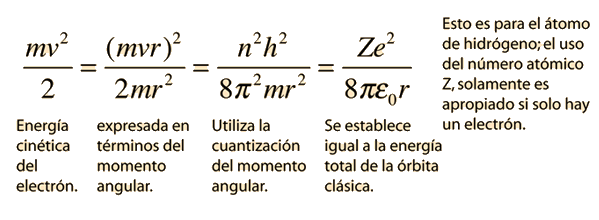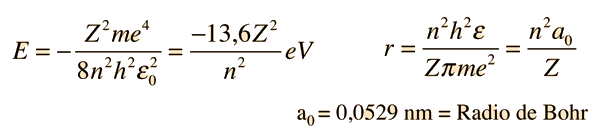Fallos del Modelo de Bohr
Aunque el modelo de Bohr fue un paso importante hacia la comprensión de la teoría cuántica del átomo, no es en realidad una descripción correcta de la naturaleza de las órbitas de electrones. Algunas de las deficiencias del modelo son:
1. No es capaz de proporcionar una comprensión de por qué ciertas líneas espectrales son más brillantes que otras. No hay ningún mecanismo para el cálculo de probabilidades de transición.
2. El modelo de Bohr trata el electrón como si se tratara de un planeta en miniatura, con un radio y momento determinado. Esto es una violación directa del principio de incertidumbre, que dicta que la posición y el momento no se pueden determinar simultáneamente.
El modelo de Bohr nos da un modelo conceptual básico de las órbitas y las energías de los electrones. Los detalles precisos de los espectros y la distribución de carga, deben dejarse en manos de los cálculos de la mecánica cuántica, como en la ecuación de Schrodinger.
|