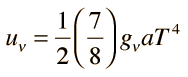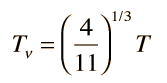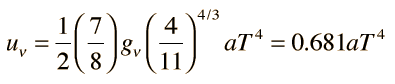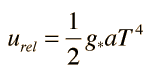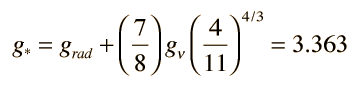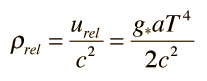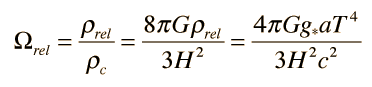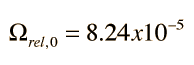Energy in Radiation in the Early Universe

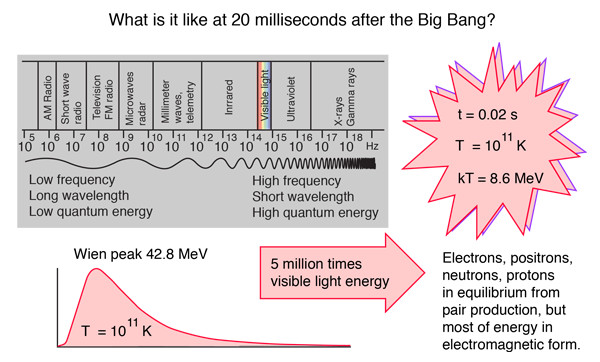
Electromagnetic radiation and the flux of neutrinos were the dominant form of energy in the early universe, becoming more dominant as one models earlier times in the big bang. It is reminiscent of the Biblical phrase "Let there be light". But of course this is not visible light but far beyond gamma rays since the average photon energy increases as one models earlier times and photon energies become high enough to accomplish pair production of all known particles. For example at a temperature of 1011 K, modeled at a time of about 20 milliseconds into Weinberg's model of the big bang, the thermal energy kT = 8.6 MeV. At this temperature, the peak energy given by the Wien displacement law is 42.8 MeV. The radiation energy was sufficient not only for electron-positron pair production, but also to maintain essentially equal populations of protons and neutrons. So in that era, radiation was truly dominant.

The radiation energy density in astronomy texts is usually put in the form

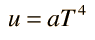
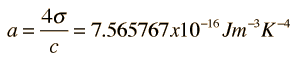
where a is called the radiation constant and has the value

For consistency with other particle quantities that are expressed in terms of the number of degrees of freedom, this is sometimes written in the form

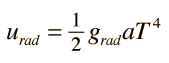
where the photon "g-factor" is grad = 2 is the number of effective degrees of freedom associated with a photon: it's polarization can be parallel or anti-parallel to its motion. This notation facilitates its combination with neutrino energy density in describing the contribution of relativistic particles to the universe's energy density.

To assess the role of radiation in the expansion of the early universe, one must take a step beyond the simple Newtonian expansion model and include the radiation pressure. When the radiation pressure is included, the effective density represented by the radiation as a function of the scale factor R is

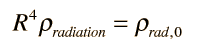
The dependence on the fourth power of R distinguishes the radiation energy density from the mass density, which depends upon the third power of R,

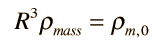
implying that the balance of mass and radiation energy density changes with the expansion of the universe, making a transition from a radiation dominated era to a mass dominated era.

Matter and radiation in the early universe
How old is the universe?
 Index

Reference
Carroll & Ostlie
Ch 29
 
HyperPhysics***** Astrophysics R Nave
 Go Back






Neutrinos in the Early Universe

Neutrinos joined Electromagnetic radiation as the dominant form of energy in the early universe, becoming more dominant as one models earlier times in the big bang. To assess the energy density in neutrinos, it would be helpful to place it in a form similar to the energy density in radiation,

but this requires a bit of analysis. For one thing, the neutrinos are fermions while the photons are bosons, so the neutrinos follow Fermi-Dirac statistics while the photons obey Bose-Einstein statistics. There are also three types of neutrinos, the electron, muon and tau neutrinos and with each is associated an antineutrino. One might expect two spin states, but one of the strange facts about neutrinos is their "chirality" - they are all "left-handed" and confined to one spin state.

Applying all the statistical factors gives a neutrino energy density expression

where gν = 6 for the 3 neutrinos plus their antiparticles, and the multiple 7/8 comes from the fact that they are fermions rather than bosons. Each of the 6 species has only one spin state.

Another difference for the neutrinos is the fact that their effective temperature at the present time is different from the 2.725K of the cosmic microwave background. Analysis of the neutrino temperature leads to the prediction that the neutrino temperature is

More detail
which puts the neutrino background at a temperature of 1.9 K. The neutrino energy expression then becomes
when stated in terms of the temperature of the electromagnetic radiation. Even though we have not been able to detect the cosmic neutrino background because of the great difficulty of neutrino detection, we are confident that it is there, and the projection of its energy density is about 68% of that of the cosmic microwave background .

Relativistic particle density
Matter and radiation in the early universe
 Index

Reference
Carroll & Ostlie
Ch 29
 
HyperPhysics***** Astrophysics R Nave
 Go Back






Relativistic Particle Density ΩRel

Neutrinos joined Electromagnetic radiation as the dominant form of energy in the early universe, becoming more dominant as one models earlier times in the big bang. In characterizing the effective density of the present universe, the mass of the neutrinos is generally neglected, and they are combined with photons as the effective density of the relativistic particles.

The combination of the radiation energy density

and the neutrino energy density
gives the total energy of the relativistic particles which can be written
where
We can now project a value for the total effective density of the relativistic particles as
and obtain a value for the density parameter Ωrel for the relativistic particles by dividing by the critical density.
This shows that the amount of energy density in the relativistic particles is very small in the present era of the universe compared to the mass density = 0.27 obtained by WMAP:
Matter and radiation in the early universe
 Index

Reference
Carroll & Ostlie
Ch 29
 
HyperPhysics***** Astrophysics R Nave
 Go Back