Mass-dominated Expansion of the Universe
In the current era, mass is dominant over radiation as a determiner of the expansion of the universe, whereas early times in the big bang were radiation-dominated. Some insight into the expansion can be obtained from a Newtonian expansion model which leads to a simplified version of the Friedman equation. Only recently have we been dealing with the fact that "dark energy" may be the dominant factor in the present expansion of the universe, but the examination of the mass-dominated expansion is important in providing insight about the current universe.
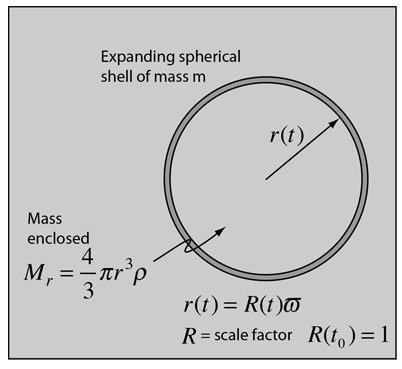 | A spherical shell of mass m which is expanding can be described in terms of its kinetic energy and gravitational potential energy, where that gravitational potential energy is contributed by the mass Mr enclosed by the sphere. The spherical shell of mass has been given an energy E. |
The simplified expansion equation is expressed in terms of the dimensionless scale factor R for the universe.
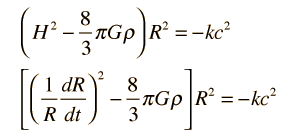
In the case where ρ = ρc, the critical density, then the curvature parameter k = 0. Since the expanding shell always contains the same amount of mass, we can write

and putting the equation in a form where it can be integrated and expressed in terms of the Hubble time tH

Then for the present time R=R0=1 the expansion time is
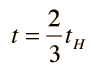
and the scale factor R is given by
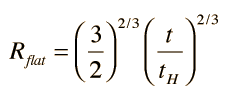
| Mass and radiation in the early universe |
| Radiation-dominated expansion |
| Relate to temperature and expansion time |
References
Carroll & Ostlie
Ch. 29
| HyperPhysics***** Astrophysics | R Nave |