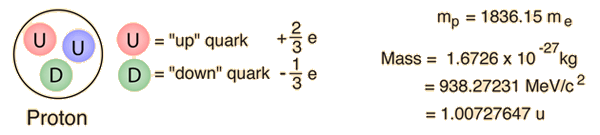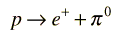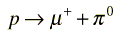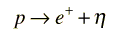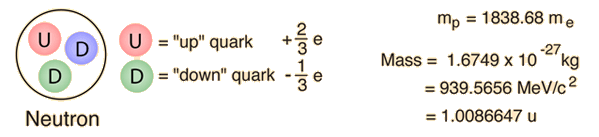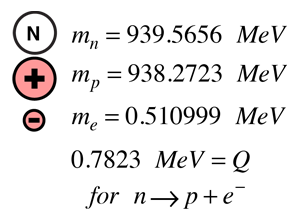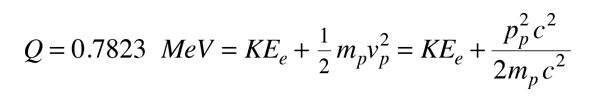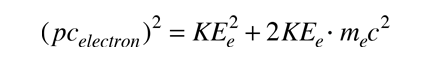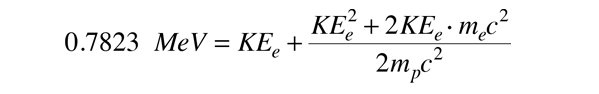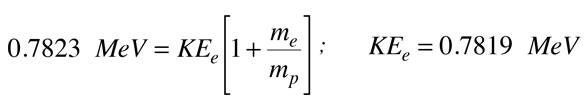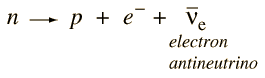Proton

Along with neutrons, protons make up the nucleus, held together by the strong force. The proton is a baryon and is considered to be composed of two up quarks and one down quark.

It has long been considered to be a stable particle, but recent developments of grand unification models have suggested that it might decay with a half-life of about 10³² years. Experiments are underway to see if such decays can be detected. Decay of the proton would violate the conservation of baryon number, and in doing so would be the only known process in nature which does so.

When we say that a proton is made up of two up quarks and a down, we mean that its net appearance or net set of quantum numbers match that picture. The nature of quark confinement suggests that the quarks are surrounded by a cloud of gluons, and within the tiny volume of the proton other quark-antiquark pairs can be produced and then annihilated without changing the net external appearance of the proton.

Proton Decay

One of the implications of the grand unification theories is that the proton should decay with a half-life on the order of 10³² years. Such a long half-life is exceedingly difficult to measure, but the hope of doing led to a deep mine experiment in the Soudan iron mines of Minnesota. The Soudan 2 Proton Decay experiment ran from 1989-2001 without observing any convincing proton decays. Such experiments serve to push back the lower bound on the proton decay halflife.

Another set of experiments designed to detect proton decay was carried out in the water Cherenkov detector at Super Kamiokande in Japan. Ed Kearns of Boston University suggested the following tentative bounds for proton decay in a review in 2001.

Decay mode for proton Suggested minimum lifetime x 1032 years 50 37 11 7.8 6.1 2.9

As of this point, it seems that the proton lifetime has been pushed out to 1033 years. The list of decay modes at left is not exhaustive. There are other modes under investigation that would suggest supersymmetry if found. Modeling the probability of detection

Neutron

Along with protons, neutrons make up the nucleus, held together by the strong force. The neutron is a baryon and is considered to be composed of two down quarks and one up quark. A free neutron will decay with a half-life of about 10.3 minutes but it is stable if combined into a nucleus. The decay of the neutron involves the weak interaction as indicated in the Feynman diagram to the right. This fact is important in models of the early universe. The neutron is about 0.2% more massive than a proton, which translates to an energy difference of 1.29 MeV.

The decay of the neutron is associated with a quark transformation in which a down quark is converted to an up by the weak interaction. The average lifetime of 10.3 min/0.693 = 14.9 minutes is surprisingly long for a particle decay that yields 1.29 MeV of energy. You could say that this decay is steeply "downhill" in energy and would be expected to proceed rapidly. It is possible for a proton to be transformed into a neutron, but you have to supply 1.29 MeV of energy to reach the threshold for that transformation. In the very early stages of the big bang when the thermal energy was much greater than 1.29 MeV, we surmise that the transformation between protons and neutrons was proceeding freely in both directions so that there was an essentially equal population of protons and neutrons.

Decay of the Neutron

A free neutron will decay with a half-life of about 10.3 minutes but it is stable if combined into a nucleus. This decay is an example of beta decay with the emission of an electron and an electron antineutrino. The decay of the neutron involves the weak interaction as indicated in the Feynman diagram to the right.

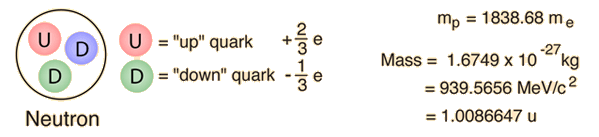
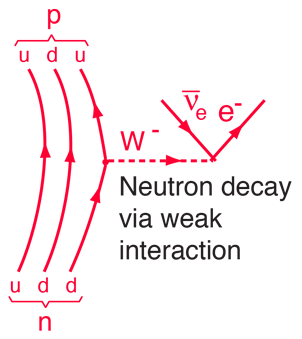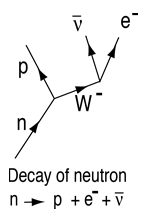
A more detailed diagram of the neutron's decay identifies it as the transformation of one of the neutron's down quarks into an up quark. It is an example of the kind of quark transformations that are involved in many nuclear processes, including beta decay.

The decay of the neutron is a good example of the observations which led to the discovery of the neutrino. An analysis of the energetics of the decay can be used to illustrate the dilemmas which faced early investigators of this process.

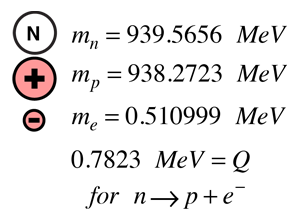
Using the concept of binding energy, and representing the masses of the particles by their rest mass energies, the energy yield from neutron decay can be calculated from the particle masses. The energy yield is traditionally represented by the symbol Q. Because energy and momentum must be conserved in the decay, it will be shown that the lighter electron will carry away most of the kinetic energy. With a kinetic energy of this magnitude, the relativistic kinetic energy expression must be used.

For the moment we presume (incorrectly) that the decay involves just the proton and electron as products. The energy yield Q would then be divided between the proton and electron. The electron will get most of the kinetic energy and will be relativistic, but the proton is non-relativistic. The energy balance is then

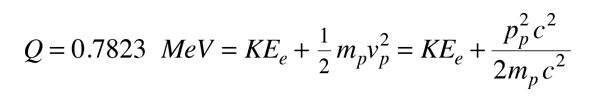
In the rest frame of the neutron, conservation of momentum requires

and pc_electron can be expressed in terms of the electron kinetic energy

Show

The energy balance then becomes

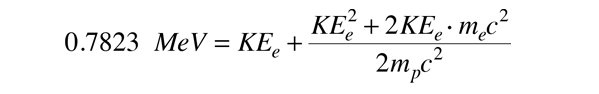
When you substitute the numbers for this value of Q, you see that the KE_e² term is negligible, so the required kinetic energy of the electron can be calculated. The required electron kinetic energy for this two-particle decay scheme is

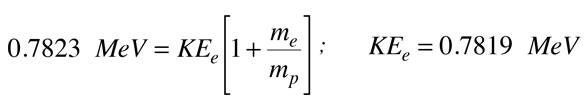
Note that the maximum kinetic energy of the recoiling proton is only about 0.4 KeV, so the recoil energies of other nuclei which have emitted beta particles is very small compared to the electron energies.

Likewise, the momentum of the electron for this two particle decay is constrained to be

Momentum and energy for the two-particle decay are constrained to these values, but this is not the way nature behaves. The observed momentum and energy distributions for the electron are as shown below.

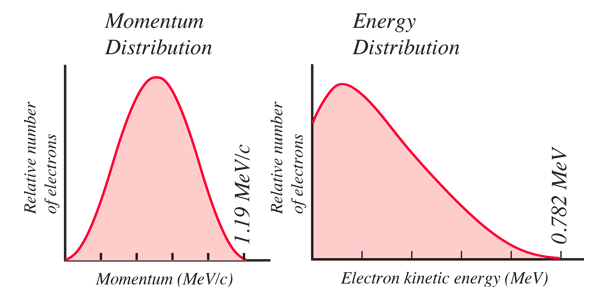
The fact that the electrons produced from the neutron decay had continuous distributions of energy and momentum was a clear indication that there was another particle emitted along with the electron and proton. It had to be a neutral particle and in certain decays carried almost all the energy and momentum of the decay. This would not have been so extraordinary except for the fact that when the electron had its maximum kinetic energy, it accounted for all the energy Q available for the decay. So there was no energy left over to account for the mass energy of the other emitted particle. The early experimenters were faced with the dilemma of a particle which could carry nearly all the energy and momentum of the decay but which had no charge and apparently no mass!

The mysterious particle was called a neutrino, but it was twenty five years before unambiguous experimental observation of the neutrino was made by Cowan and Reines. The present understanding of the decay of the neutron is

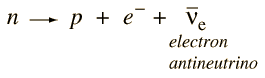
This decay illustrates some of the conservation laws which govern particle decays. The proton in the product satisfies the conservation of baryon number, but the emergence of the electron unaccompanied would violate conservation of lepton number. The third particle must be an electron antineutrino to allow the decay to satisfy lepton number conservation. The electron has lepton number 1, and the antineutrino has lepton number -1.