The Age of the Universe
How old is the universe? This provocative question will be addressed only by describing the models we have of the expanding universe and the Big Bang process. If we could take the presently observed expansion and project backward to the beginning of that process, then it would seem reasonable to call that the age of the universe.
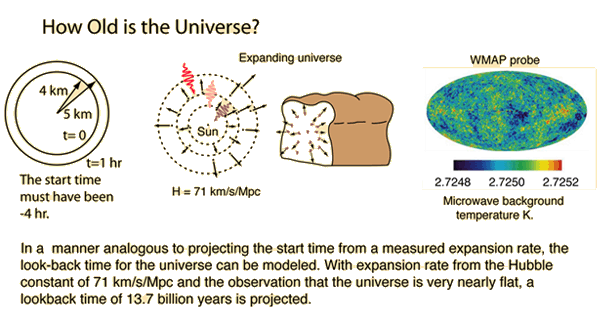
If we were dealing with a simple expansion as suggested at left in the illustration, and could measure the expansion as a function of time, then it might be straightforward to calculate the time of origin of the expansion. But our time span of observation is so brief compared to the process as a whole that we must draw our conclusions from an almost instantaneous view. We can see clear evidence of expansion from the Doppler red shift, and the fact that more distant stars are redshifted more. The Hubble law and the value of the Hubble constant give us a parameter that we can translate into an expansion time but there are other factors involved. Because of the uncertainties in distance measurement to other galaxies, there have been considerable uncertainties about the value of the Hubble constant.
Recent measurements of the cosmic background radiation by the COBE and WMAP satellites have provided values of the Hubble constant which are much more precise.
Even with the a known value for the Hubble constant, the value projected for the age of the universe is model dependent. Much evidence suggests that the universe is very nearly "flat", i.e., it is expanding at just about the right rate to expand indefinitely. Perfectly flat would mean that it would asymptotically approach a zero expansion rate, and not collapse back. A flat universe, termed an "Einstein-de Sitter universe" requires a critical mass density. We presume that we have very close to that critical mass density, but it is much more than the mass density we see, hence the presumption of "dark matter" to make up the bulk of the critical mass.
With the presumption of a flat universe, we can project an expansion time by making use of the current cosmic background temperature and the critical mass density of the universe. For a Hubble constant of 71 km/s/Mpc the critical density is 5.33 GeV/m3. When this is substituted into the equation for expansion time you get 13.77 x 109 years.
| Calculation of expansion time |
| A brief overview of time. |
| HyperPhysics***** Astrophysics | R Nave |