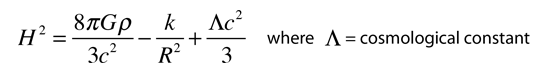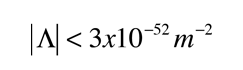The Friedmann Equation
Alexander Friedmann of Russia is credited with developing a dynamic equation for the expanding universe in the 1920s. This was a time when Einstein, Willem de Sitter of the Netherlands, and Georges Lemaitre of Belgium were also working on equations to model the universe. Friedmann developed it as a relativistic equation in the framework of general relativity, but the description here will be limited to a simplified, non-relativistic version based on Newton's laws.
Convenient forms of Friedmann's equation with which to examine the expansion time and temperature for a big bang model of the universe are
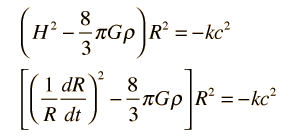
Besides the density and gravitation constant G, the equation contains the Hubble parameter H, a scaling parameter R, and a factor k which is called the curvature parameter. The curvature parameter indicates whether the universe is open or closed. The above equations do not specify the nature of the density ρ. They do not include any particle interactions other than gravitational attraction. Such particle interactions, like collisions, could be specified in terms of pressure, so the model above is sometimes referred to as a "pressureless" universe. More detailed versions of the Friedman equation include such effects.
Einstein considered adding another term, the famous (or infamous) cosmological constant which would produce a static universe.
| Relate to temperature and expansion time |
References
Rohlf
Ch. 19
Kaufmann
Ch. 28
| HyperPhysics***** Astrophysics | R Nave |