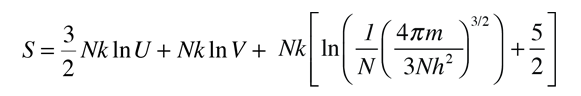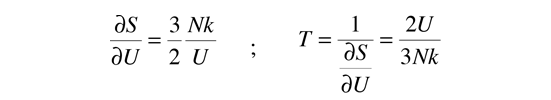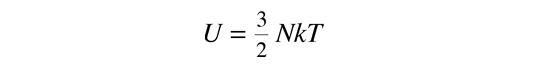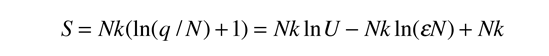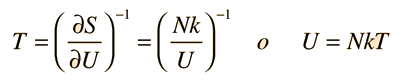Una Visión mas General de la Temperatura

Cuando un objeto con temperatura alta, se coloca en contacto con otro objeto a baja temperatura, la energía fluye desde el objeto con alta temperatura hacia el objeto con mas baja temperatura, hasta que ambos alcanzan el equilibrio térmico. Cuando se examinan los detalles de este escenario común, se hace evidente que la simple visión de la temperatura que vemos incorporada en el uso común de la temperatura cinética, presenta algunos problemas.

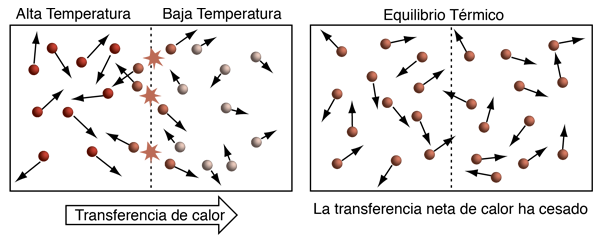
Cuando la temperatura cinética proporciona una descripción general razonable sobre la naturaleza de la temperatura, la ilustración de arriba resume la situación. En los gases monoatómicos actuando como masas puntuales, una mayor temperatura significa simplemente mayor energía cinética media. Las moléculas mas rápidas, chocando en colisiones elásticas contra las mas lentas en su borde de unión, aumentará la velocidad de estas últimas y disminuirá la velocidad de las primeras, transfiriendo energía desde la región de temperatura alta hacia la de temperatura mas baja. Con el tiempo, las moléculas en las dos regiones, alcanzarán la misma energía cinética media (misma temperatura) y en esta condición de equilibrio térmico, no habrá ninguna transferencia mas de energía neta desde un objeto hacia el otro.

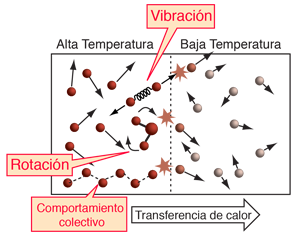El concepto de temperatura se complica por los grados de libertad internos, como la rotación y la vibración molecular y por la existencia de interacciones internas en los materiales sólidos, los cuales incluyen los modos colectivos de oscilación. Los movimientos internos de las moléculas, afectan al calor específico de los gases. El caso clásico es el hidrógeno diatómico. Los modos colectivos afectan a los calores específicos de sólidos, particularmente a baja temperatura.

Complicaciones como esta, han determinado la adopción de un enfoque diferente para el concepto de temperatura en el estudio de la termodinámica. La proposición de Schroeder de la definición teórica de temperatura es:

• "La temperatura es una medida de la tendencia de un objeto a ceder espontáneamente energía hacia su entorno. Cuando dos objetos están en contacto interno, el que tiende espontáneamente a perder energía está a temperatura mas alta."(Thermal Physics, Cap. 1.)

La temperatura cinética de los gases ideales monoatómicos descritos arriba, es consistente con esta definición de temperatura para los sistema simples a los que se aplica. En ese caso el equilibrio alcanzado es donde se da la máxima entropía, y la velocidad en alcanzar ese estado, será proporcional a la diferencia de temperaturas entre las dos partes del sistema. Debemos notar que el estado de equilibrio de una colección de partículas, será el estado de la máxima multiplicidad, por lo que se puede definir la temperatura en términos de esa multiplicidad (entropía) como sigue:

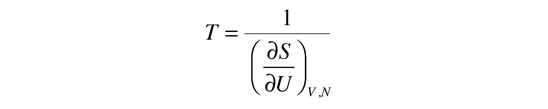
La temperatura se expresa como el inverso de la velocidad de cambio de la entropía con respecto a la energía interna, manteniendo el volumen y el número de partículas constantes. Ciertamente, esto no es tan intuitivo como la energía cinética molecular, pero en las aplicaciones termodinámicas es mas fiable y mas general.

La Relación de la Entropía con la Temperatura

En los estudios de termodinámica introductorios, se usa normalmente la definición de temperatura en términos de la energía cinética molecular, la "temperatura cinética". Pero en vista de las dificultades prácticas con ese enfoque, a menudo se define la temperatura en función de otras dos variables de estado, la entropía S y la energía interna U.

La temperatura se expresa como el inverso de la velocidad de cambio de la entropía con respecto a la energía interna, manteniendo el volumen y el número de partículas constantes. Ciertamente, esto no es tan intuitivo como la energía cinética molecular, pero en las aplicaciones termodinámicas es mas fiable y mas general. Esta fórmula de la temperatura se puede obtener de la identidad termodinámica.

Para aplicar esta definición de temperatura a un gas ideal monoatómico, necesitamos una expresión para la entropía de un gas ideal:

Luego, usando la definición de temperatura en términos de la entropía:

Esto da una expresión de la energía interna que es consistente con la equipartición de energía.

con kT/2 de energía para cada grado de libertad de cada átomo.

Otro ejemplo de este enfoque de la temperatura es el sólido de Einstein con q unidades de energía y N osciladores. La energía interna U se puede representar por q multiplicado por la unidad de energía del oscilador hf= e. La entropía se puede expresar como

Tomando la derivada da

Esto es lo que se espera de la equipartición de energía. Cada oscilador tiene dos grados de libertad y cada uno representa kT/2 de energía, dando U=NkT.