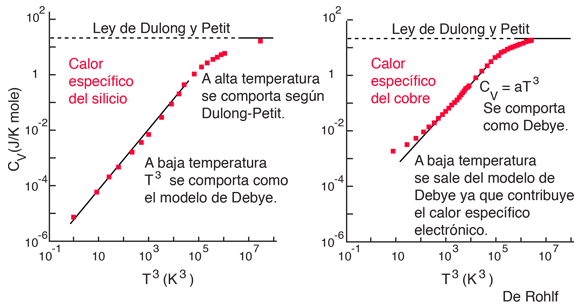
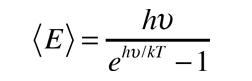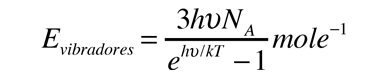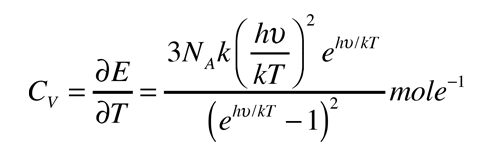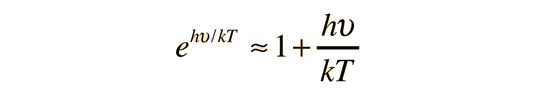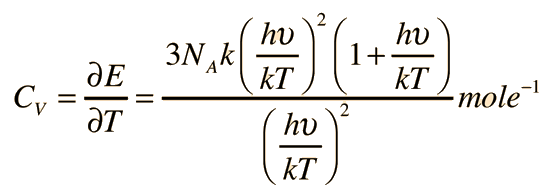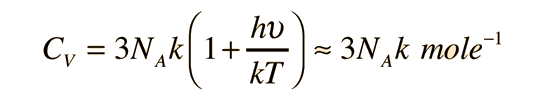Ley de Dulong y Petit
El calor específico del cobre es 0,093 cal/gm ºK (0,389 J/gm ºK) y el del plomo es solamente 0,031 cal/gm ºK (0,13 J/gm ºK). ¿Por que son tan diferentes?. La diferencia radica principalmente en que están expresados como energía por unidad de masa; si lo expresamos como energía por moles, son muy similares. La ley de Dulong y Petit, trata de la similitud de los calores específicos molares de los metales. La similitud se puede explicar mediante la aplicación de la equipartición de la energía, a los átomos de los sólidos.
A partir de sólo los grados de libertad de desplazamiento, se consigue 3kT/2 de energía por átomo. La energía añadida a los sólidos, toma la forma de vibraciones atómicas, y esto contribuye con tres grados adicionales de libertad, y una energía total por átomo de 3kT. El calor específico a volumen constante, debería ser exactamente la proporción de cambio de esa energía con la temperatura (derivada respecto de la temperatura).

Cuando se analiza sobre una base molar, el calor específico del cobre y el plomo son muy similares:

|
Índice |