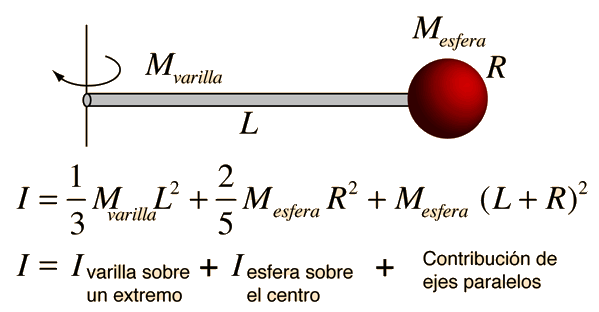
Momento de Inercia: Disco Delgado
El momento de inercia de un fino disco circular, es el mismo que el del cilindro sólido de cualquier longitud, pero que merece una consideración especial, porque a menudo se usa como un elemento para la construcción de expresiones de momentos de inercia para otras geometrías, tales como la esfera o el cilindro sobre un diámetro de un extremo. El momento de inercia sobre un diámetro, es el ejemplo clásico del teorema de los ejes perpendiculares. Para un objeto plano:
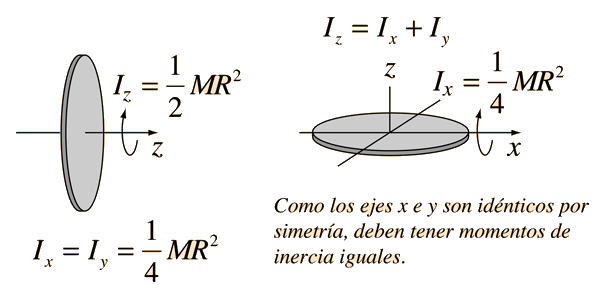
Conceptos sobre Momento de Inercia
| HyperPhysics*****Mecánica*****Rotación | M Olmo R Nave |