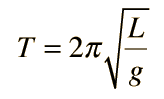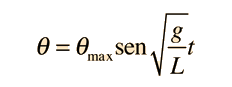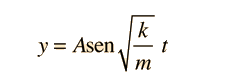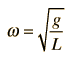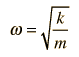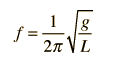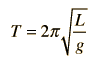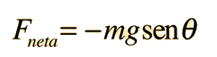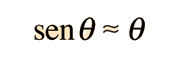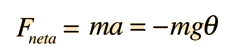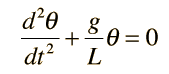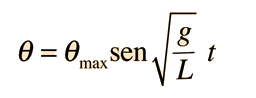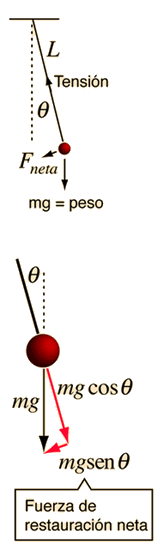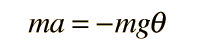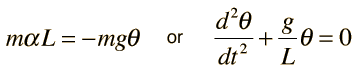Péndulo Simple

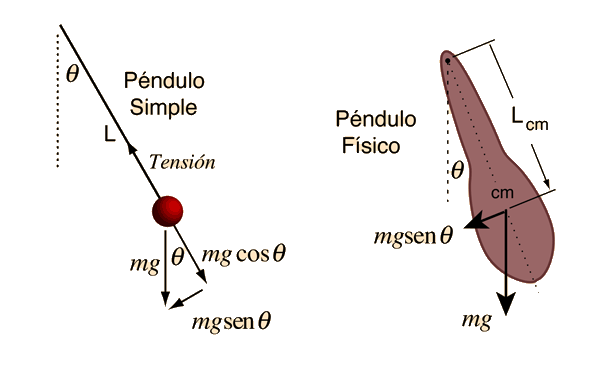
Un péndulo simple es uno tal, que se puede considerar como una masa puntual, suspendida de una cuerda o varilla de masa despreciable. Es un sistema resonante con una frecuencia de resonancia simple. Para pequeñas amplitudes, el periodo de tal péndulo, se puede aproximar por:

Mostrar Para una longitud de péndulo L = cm = m y una aceleración de la gravedad g = m/s2 el periodo del péndulo es T = s (Entrar datos para dos de las variables y luego haga clic sobre el texto activo de la tercera variable a calcular.) Esta expresión del periodo es razonablemente exacta para ángulos de unos pocos grados, pero el tratamiento del péndulo de amplitud grande es mucho mas complejo.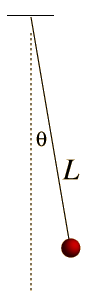

Si la vara no tiene una masa despreciable, entonces debe ser tratada como un péndulo físico.

Sean Carroll relata la historia del descubrimiento de Galileo sobre el hecho de que para pequeñas amplitudes, el período y la frecuencia no se ven afectados por la amplitud. "Según se informa, en 1581, un joven Galileo Galilei hizo un descubrimiento revolucionario mientras estaba sentado y aburrido durante un servicio religioso en una iglesia de Pisa. La araña que pendia del techo sobre su cabeza, oscilaba suavemente hacia atrás y hacia delante, pero parecia moverse más rápidamente cuando el balanceo era más amplio (por ejemplo, después de una ráfaga de viento), y más lentamente cuando el balanceo era más corto. Intrigado, Galileo decidió medir el tiempo que duraba cada oscilación, utilizando para ello el único evento aproximadamente periódico al que tenia fácil acceso: los latidos de su propio pulso. Encontró algo interesante: el número de latidos del corazón entre los vaivenes de la araña era más o menos el mismo, independientemente de si las oscilaciones eran anchas o estrechas. El tamaño de las oscilaciones - la amplitud del recorrido del péndulo hacia adelante y hacia atrás-, no afectaba a la frecuencia de estas oscilaciones.

Movimiento del Péndulo

El movimiento de un péndulo simple es como un movimiento armónico simple en donde la ecuación para el desplazamiento angular es

Mostrar Que tiene la misma forma que el movimiento de una masa sobre un muelle: La frecuencia angular del movimiento está dada por comparada a para una masa sobre un muelle.

La frecuencia del péndulo en Hz está dada por

y el periodo del movimiento es entonces

Periodo de Péndulo Simple

Una masa puntual colgando de una cuerda sin masa, es un ejemplo idealizado de un péndulo simple. Cuando se desplaza desde su punto de equilibrio, la fuerza de restauración que lo trae de nuevo al centro, está dada por:

Mostrar Para pequeños ángulos θ, podemos usar la aproximación Mostrar en cuyo caso la segunda ley de Newton toma la forma Aún en este caso aproximado, la solución de la ecuación hace uso de las ecuaciones y cálculo diferencial. La ecuación diferencial es y para pequeños ángulos θ la solución es:

Geometría del Péndulo

Ecauciones del Péndulo

La ecuación de movimiento para el péndulo simple para amplitudes suficientemente pequeñas tiene la forma

La cual, cuando se pone en forma angular viene a ser Esta ecuación diferencial es como la del oscilador armónico simple y tiene la solución: