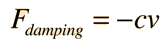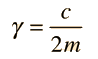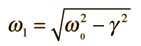Oscilador Armónico Amortiguado

Coeficiente de Amortiguación Oscilador No Amortiguado Oscilador Impulsado

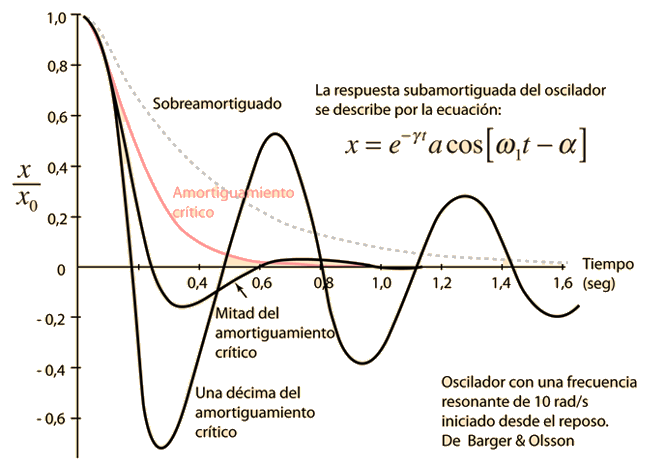
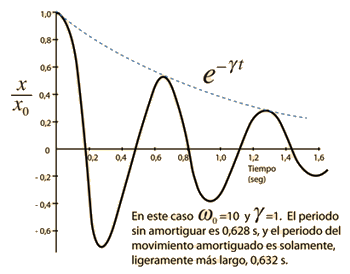
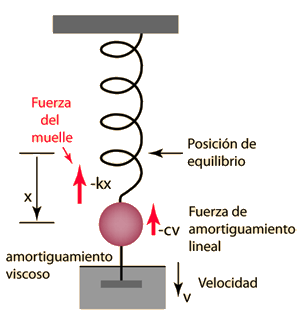
La ecuación del movimiento de la 2ª Ley de Newton es 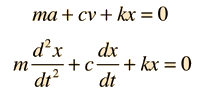Esto está en forma de una ecuación diferencial homogénea de segundo orden, y tiene una solución de la forma 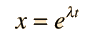Sustituyendo esto en la fórmula, da la ecuación auxiliar de λ 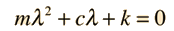Las raices de la ecuación auxiliar cuadrática son 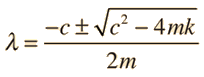Los tres casos resultantes para el oscilador amortiguado son

Coeficiente de amortiguación

Cuando un oscilador amortiguado está sujeto a una fuerza de amortiguación que es linealmente dependiente de la velocidad, tales como una amortiguación viscosa, el oscilador tendrá términos de decaimiento exponencial, que depende del coeficiente de amortiguación. Si la fuerza de amortiguación es de la forma

entonces, el coeficiente de amortiguación está dado por

Esto parece lógico cuando se observa que la fuerza de amortiguación es proporcional a c, y está influenciada inversamente proporcional por la masa del oscilador.

Oscilador Subamortiguado

Oscilador Subamortiguado

La ecuación es la de una sinusoide que decae exponencialmente. El coeficiente de amortiguación es menor que la frecuencia de resonancia sin amortiguar . La frecuencia de resonancia está dada por pero el movimiento no es estrictamente periódico.