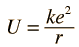Temperatura Crítica de Ignición para la Fusión
La temperatura de fusión obtenida al establecer la energía térmica promedia, igual a la barrera de Coulomb, da una temperatura demasiado alta, porque la fusión puede ser iniciada por aquellas partículas que están fuera de la cola de alta energía, de la distribución de Maxwell para las energías de las partículas. La temperatura crítica de ignición se reduce aún más, por el hecho de que algunas partículas que tienen energías por debajo de la barrera de Coulomb, puede atravesar la barrera por efecto túnel.
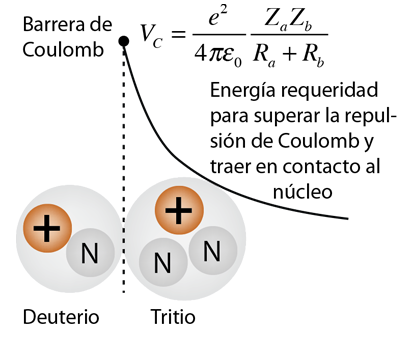
La presunta altura de la barrera de Coulomb, se basa en la distancia a la que la fuerza nuclear fuerte podría superar la repulsión de Coulomb. La temperatura requerida puede ser sobreestimada si se utilizan para esta distancia los radios clásicos de los núcleos, ya que el rango de la interacción fuerte, es significativamente mayor que el radio clásico del protón.
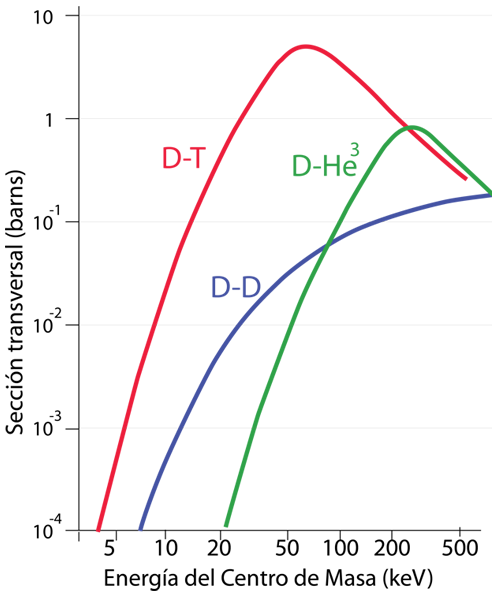
Al tratar de modelar la probabilidad de fusión nuclear, el enfoque típico es modelarlo como una "sección transversal" para que ocurra la reacción. Este enfoque es quizá más evidente en la evaluación de la dispersión de partículas como en la dispersión de Rutherford, pero a menudo también se utiliza el lenguaje para la fusión nuclear. Para los propósitos de aquí, se puede tomar la sección transversal para significar la probabilidad de que ocurra la fusión nuclear. Modelar esta sección implica tener en cuenta la probabilidad del efecto túnel a través de la barrera de Coulomb. Esta probabilidad es mayor para las partículas de energía más alta, pero debido a la distribución de Maxwell, hay menos de estas partículas de alta energía. Además, la energía efectiva de colisión entre partículas para la fusión depende de sus velocidades relativas, por lo que el cálculo del modelo para la producción de fusión nuclear implica un promedio sobre todas las velocidades relativas. Los resultados de tal modelado se presentan como un trazado de la sección transversal de fusión en función de la energía de partícula media.
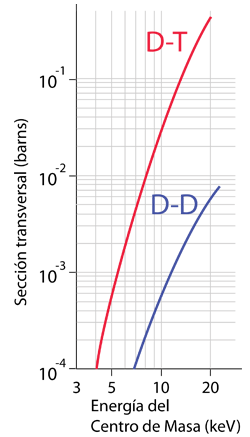 |
Con todas estas consideraciones, los requerimientos energéticos para la fusión nuclear de deuterio-tritio y deuterio-deuterio son dramáticamente inferiores a la barrera de Coulomb, pero son sin embargo muy difíciles de alcanzar de manera controlada.
Las referencias sugieren que las energías de partícula actualmente alcanzables en los reactores termonucleares está en el rango de 1 - 10 keV. Si se sustituyen esas energías en la relación de energía térmica, entonces 1keV corresponde a una temperatura de 0,77 x 107K y 10 keV corresponde a una temperatura de 0,77 x 108K.
|
El TFTR alcanzó una temperatura de 5,1 x 108 K, bastante superior a la temperatura crítica de ignición de la fusión D-T.
|
Índice
Conceptos de Fusión |