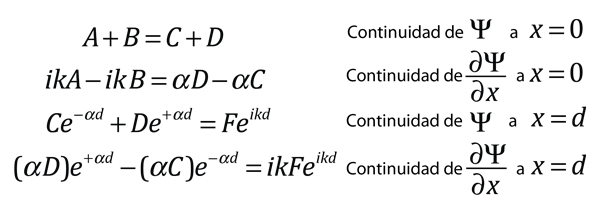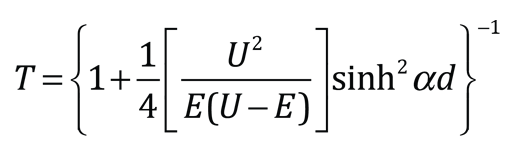Penetración de Barrera

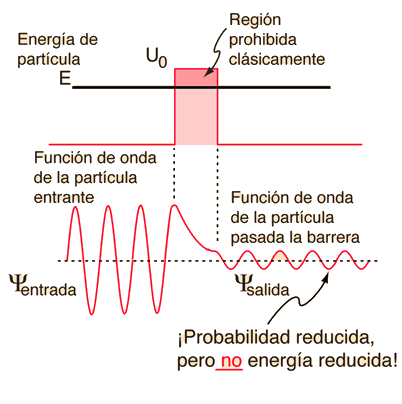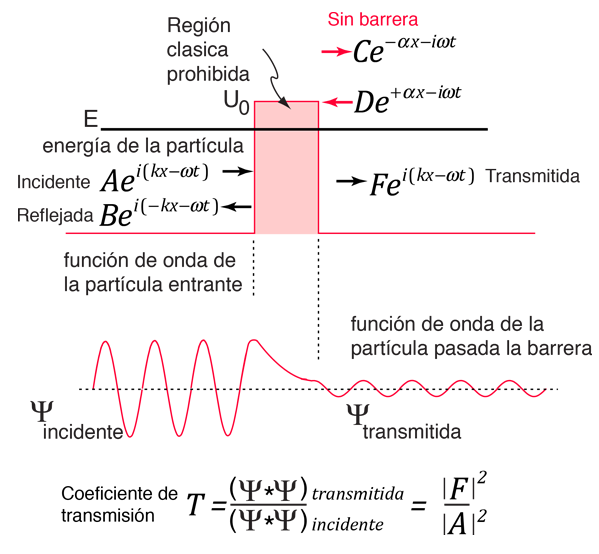
Según la física clásica, una partícula con energía E inferior a la altura U₀ de una barrera, no penetraría -la región del interior de la barrera está clásicamente prohibida-. Pero la función de onda asociada a una partícula libre, debe ser continua en la barrera, y mostrará un decaimiento exponencial dentro de la barrera. La función de onda, también debe ser continua en el otro lado de la barrera, así que hay una probabilidad finita de que la partícula, penetrará a través de la barrera.

Cuando una partícula se aproxima a la barrera, se describe por una función de onda de partícula libre. Cuando alcanza la barrera, debe satisfacer la ecuación de Schrödinger en la forma

que tiene la solución

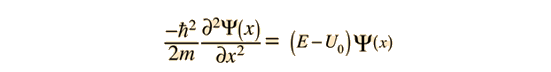
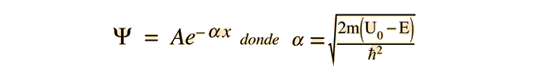
Nótese que además de la masa y la energía de la partícula, existe una dependencia de la constante de física fundamental h, la constante de Planck. La constante de Planck aparece en la hipótesis de Planck, donde dá valores discretos a la energía cuántica del fotón, y aparece en los niveles de energía atómica, que se calculan utilizando la ecuación de Schrodinger.

Hay circunstancias en las que se puede obtener una aproximación razonable del coeficiente de transmisión a través de la barrera simplemente tomando el cuadrado de la relación de las amplitudes de las funciones de onda en la salida y la entrada de la barrera. Esa aproximación al coeficiente de transmisión se puede expresar como:

Esta aproximación se evaluará a continuación y se comparará con un tratamiento mecánico cuántico más riguroso.

Si una partícula de energía E =x10^ julios = eV =MeV =GeV

y masa

m = x 10^ kg = m_e = m_p = MeV/c²,

se aproxima a una barrera de altura

U₀ = x 10^ julios = eV= MeV,

y grosor

d = x 10^ m = nm= fermi,

entonces, el factor de atenuación es

α = x10^ 1/m .

y la proporción entre las amplitudes saliente y entrante es x10^ .

Como la probabilidad es proporcional al cuadrado de la amplitud, la probabilidad de efecto túnel (penetración de barrera) es = x10^ .

Este enfoque aproximado del coeficiente de transmisión a través de la barrera se usó en la introducción a la desintegración alfa, que procede mediante un túnel mecánico cuántico a través de la barrera de Coulomb, y se usó para aproximar la vida media de desintegración del polonio.

La precisión de este enfoque aproximado no es suficiente para aplicaciones de tunelización en electrónica de estado sólido, donde se puede tratar con el tunelizado del flujo de electrones a través de capas aislantes muy delgadas. El tratamiento más riguroso del coeficiente de transmisión da la expresión

Usando el requisito más riguroso de continuidad tanto de la función de onda como de su primera derivada en ambos límites, el coeficiente de transmisión para la barrera descrita anteriormente se convierte en T = x10^ .

Barrera del Decaimiento Alfa

Índice

Conceptos de la Ecuación de Schrödinger

HyperPhysics*****Física Cuántica

M Olmo R Nave

Atrás

Penetración de Barrera Mecánica Cuántica

Según la física clásica, una partícula de energía E menor que la altura U0 de una barrera no podría penetrar; la región dentro de la barrera está clásicamente prohibida. Pero la función de onda asociada con una partícula libre debe ser continua en la barrera y mostrará una disminución exponencial dentro de la barrera. La función de onda también debe ser continua en el lado más alejado de la barrera, por lo que existe una probabilidad finita de que la partícula atraviese la barrera. Además de ser continua en la entrada y salida de la barrera, la primera derivada de la función de onda también debe ser continua en la entrada y salida de la barrera. Dado que la probabilidad de detectar la partícula es proporcional al cuadrado de la función de onda, el coeficiente de transmisión a través de la barrera es proporcional al cuadrado de la función de onda transmitida dividido por el cuadrado de la función de onda incidente. Pero dado que la función de onda puede reflejarse desde la primera y segunda superficies de la barrera, derivar la expresión del coeficiente de transmisión es un ejercicio matemático no trivial.

La resolución del coeficiente de transmisión requiere la evaluación de las condiciones de contorno en la superficie de la barrera.

Las ecuaciones se pueden dividir por A, ya que establece la escala para las otras amplitudes. Eso da cuatro ecuaciones con cuatro incógnitas que se pueden resolver mediante sustituciones repetidas. La ecuación única resultante para el coeficiente de transmisión se puede expresar en términos de los parámetros conocidos de la barrera.

El coeficiente de transmisión se puede obtener en el cálculo de Javascript anterior.

Barrera en el Decaimiento Alfa

Índice

Conceptos de la ecuación de Schrodinger

Beiser
Moderns Physics Concepts,
Cap. 5

Serway, Moses, Moyer
Modern Physics, 2nd Ed
Cap. 6

HyperPhysics*****Física Cuántica

M Olmo R Nave

Atrás