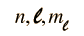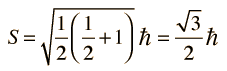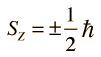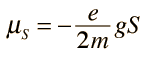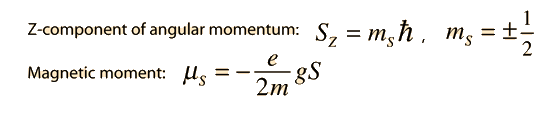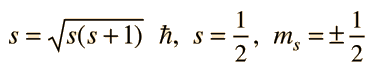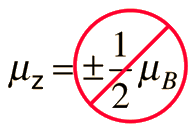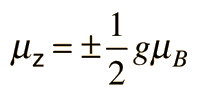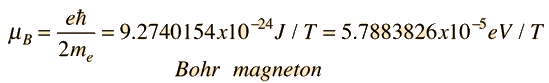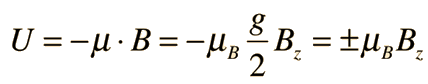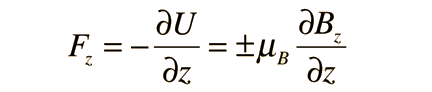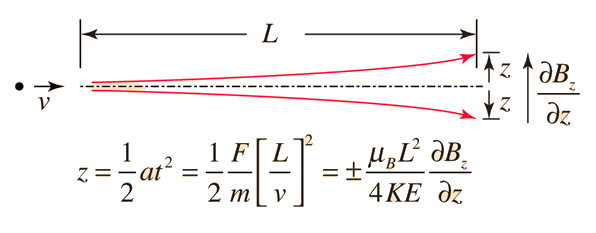Electron Spin

Spin "up" and "down" allows two electrons for each set of spatial quantum numbers.

An electron spin s = 1/2 is an intrinsic property of electrons. Electrons have intrinsic angular momentum characterized by quantum number 1/2. In the pattern of other quantized angular momenta, this gives total angular momentum The resulting fine structure which is observed corresponds to two possibilities for the z-component of the angular momentum. This causes an energy splitting because of the magnetic moment of the electron

Electron Spin

Two types of experimental evidence which arose in the 1920s suggested an additional property of the electron. One was the closely spaced splitting of the hydrogen spectral lines, called fine structure. The other was the Stern-Gerlach experiment which showed in 1922 that a beam of silver atoms directed through an inhomogeneous magnetic field would be forced into two beams. Both of these experimental situations were consistent with the possession of an intrinsic angular momentum and a magnetic moment by individual electrons. Classically this could occur if the electron were a spinning ball of charge, and this property was called electron spin.

Quantization of angular momentum had already arisen for orbital angular momentum, and if this electron spin behaved the same way, an angular momentum quantum number s = 1/2 was required to give just two states. This intrinsic electron property gives:

Electron Intrinsic Angular Momentum

Experimental evidence like the hydrogen fine structure and the Stern-Gerlach experiment suggest that an electron has an intrinsic angular momentum, independent of its orbital angular momentum. These experiments suggest just two possible states for this angular momentum, and following the pattern of quantized angular momentum, this requires an angular momentum quantum number of 1/2.

With this evidence, we say that the electron has spin 1/2. An angular momentum and a magnetic moment could indeed arise from a spinning sphere of charge, but this classical picture cannot fit the size or quantized nature of the electron spin. The property called electron spin must be considered to be a quantum concept without detailed classical analogy. The quantum numbers associated with electron spin follow the characteristic pattern:

Illustration

Electron Spin Magnetic Moment

Since the electron displays an intrinsic angular momentum, one might expect a magnetic moment which follows the form of that for an electron orbit. The z-component of magnetic moment associated with the electron spin would then be expected to be

The electron spin magnetic moment is important in the spin-orbit interaction which splits atomic energy levels and gives rise to fine structure in the spectra of atoms. The electron spin magnetic moment is also a factor in the interaction of atoms with external magnetic fields (Zeeman effect).

The term "electron spin" is not to be taken literally in the classical sense as a description of the origin of the magnetic moment described above. To be sure, a spinning sphere of charge can produce a magnetic moment, but the magnitude of the magnetic moment obtained above cannot be reasonably modeled by considering the electron as a spinning sphere. High energy scattering from electrons shows no "size" of the electron down to a resolution of about 10^-3 fermis, and at that size a preposterously high spin rate of some 10³² radian/s would be required to match the observed angular momentum.

Stern-Gerlach Experiment

This experiment confirmed the quantization of electron spin into two orientations. This made a major contribution to the development of the quantum theory of the atom.

The potential energy of the electron spin magnetic moment in a magnetic field applied in the z direction is given by

where g is the electron spin g-factor and m_B is the Bohr magneton.

Using the relationship of force to potential energy gives

The deflection can be shown to be proportional to the spin and to the magnitude of the magnetic field gradient. It is inversely proportional to the particle kinetic energy.

Stern-Gerlach Experiment

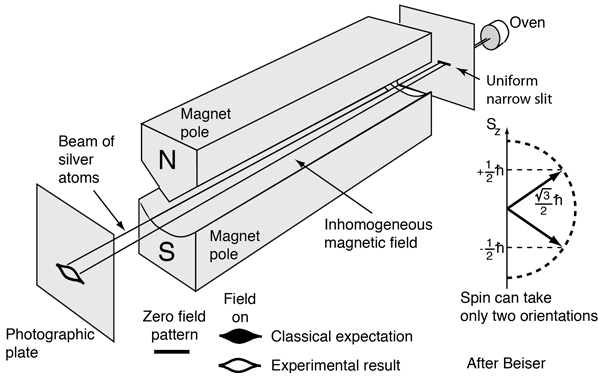
In 1921, Otto Stern and Walter Gerlach performed an experiment which showed the quantization of electron spin into two orientations. This made a major contribution to the development of the quantum theory of the atom.

The actual experiment was carried out with a beam of silver atoms from a hot oven because they could be readily detected using a photographic emulsion. The silver atoms allowed Stern and Gerlach to study the magnetic properties of a single electron because these atoms have a single outer electron which moves in the Coulomb potential caused by the 47 protons of the nucleus shielded by the 46 inner electrons. Since this electron has zero orbital angular momentum (orbital quantum number l=0), one would expect there to be no interaction with an external magnetic field.

Stern and Gerlach directed the beam of silver atoms into a region of nonuniform magnetic field (see experiment sketch). A magnetic dipole moment will experience a force proportional to the field gradient since the two "poles" will be subject to different fields. Classically one would expect all possible orientations of the dipoles so that a continuous smear would be produced on the photographic plate, but they found that the field separated the beam into two distinct parts, indicating just two possible orientations of the magnetic moment of the electron.

But how does the electron obtain a magnetic moment if it has zero angular momentum and therefore produces no "current loop" to produce a magnetic moment? In 1925, Samuel A. Goudsmit and George E. Uhlenbeck postulated that the electron had an intrinsic angular momentum, independent of its orbital characteristics. In classical terms, a ball of charge could have a magnetic moment if it were spinning such that the charge at the edges produced an effective current loop. This kind of reasoning led to the use of "electron spin" to describe the intrinsic angular momentum.