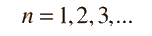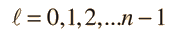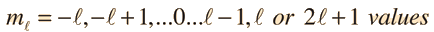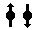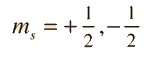Geometry of Hydrogen Atom Solution
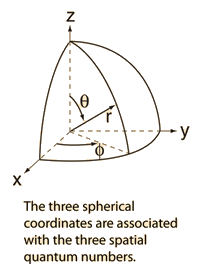
The hydrogen atom solution to the Schrodinger equation produces three quantum numbers which can be seen to arise naturally from geometrical constraints on the wavefunction.
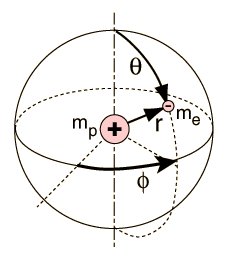
|
Separated into equations in terms of the spherical coordinates 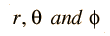 the wavefunction takes the form 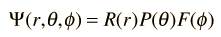 which gives three equations. The equation for each of the three variables gives rise to a quantum number and the quantized energy states of the atom can be specified in terms of these quantum numbers. |
Hydrogen concepts
| HyperPhysics***** Quantum Physics | R Nave |