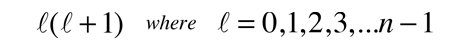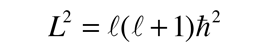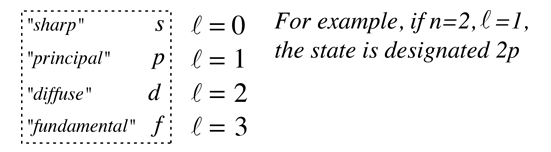The Colatitude Equation

Upon separation of the Schrodinger equation for the hydrogen atom, the colatitude equation is:

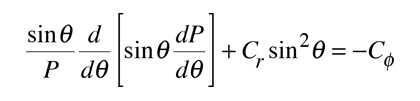
The solution of the azimuthal equation provides the constraint

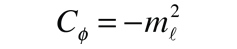
A detailed solution involves conversion of the above equation to a form in which the variable is cos θ . It can be solved by a series expansion (polynomial) method in which the conditions for a solution force the remaining constant to be of the form

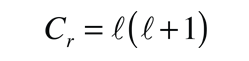
producing the orbital quantum number. The solutions to the colatitude equation are in a form called associated Legendre functions, and when properly normalized form part of the hydrogen wavefunctions.

The Orbital Quantum Number

From constraints on the behavior of the hydrogen wavefunction in the colatitude equation arises a constant of the form

where n is the principal quantum number. This defines the orbital quantum number, which determines the magnitude of the orbital angular momentum in the relationship

This relationship between the magnitude of the angular momentum and the quantum number is commonly visualized in terms of a vector model. The orbital quantum number determines the bounds on the magnetic quantum number. The orbital quantum number is used as a part of the designation of atomic electron states in the spectroscopic notation.

The orbital quantum number plays a role in the Zeeman interaction since the orbital motion contributes a magnetic moment, and is important as an indicator of subshell differences in electron energies.

Spectroscopic Notation

Before the nature of atomic electron states was clarified by the application of quantum mechanics, spectroscopists saw evidence of distinctive series in the spectra of atoms and assigned letters to the characteristic spectra. In terms of the quantum number designations of electron states, the notation is as follows:

The spectroscopic notation is extended to create term symbols for the electronic states of multi-electron atoms. In doing so, the scheme used for the orbital angular momentum of a single electron above is applied to the total orbital angular momentum L associated with the electron state.