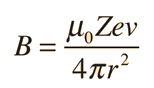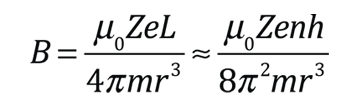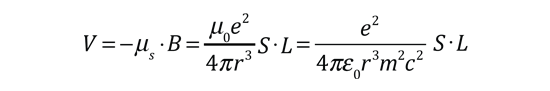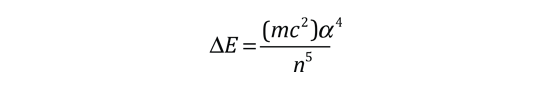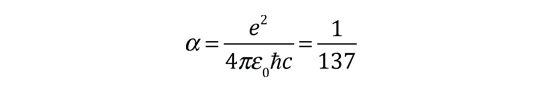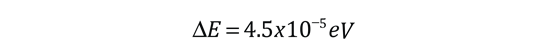Hydrogen Fine Structure
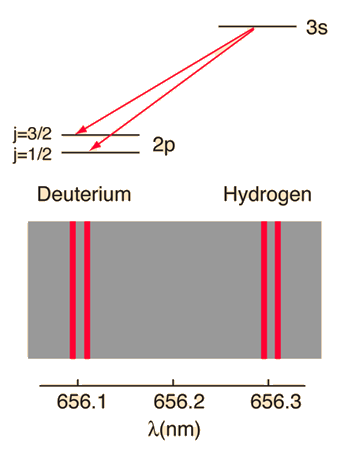
When the familiar red spectral line of the hydrogen spectrum is examined at very high resolution, it is found to be a closely-spaced doublet. This splitting is called fine structure and was one of the first experimental evidences for electron spin.
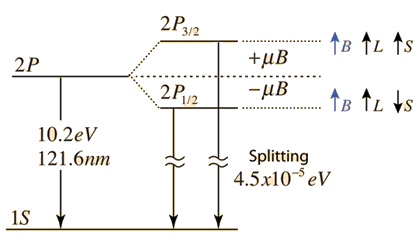
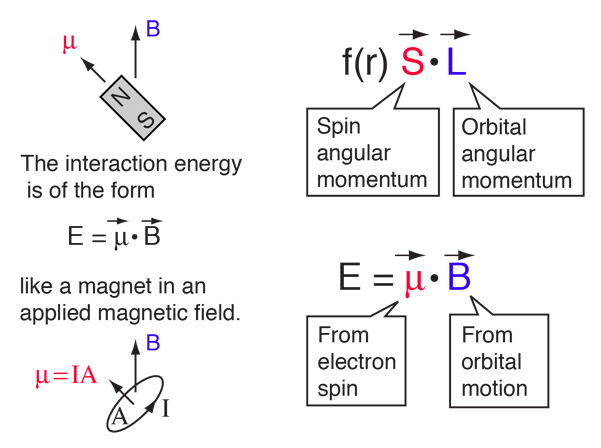
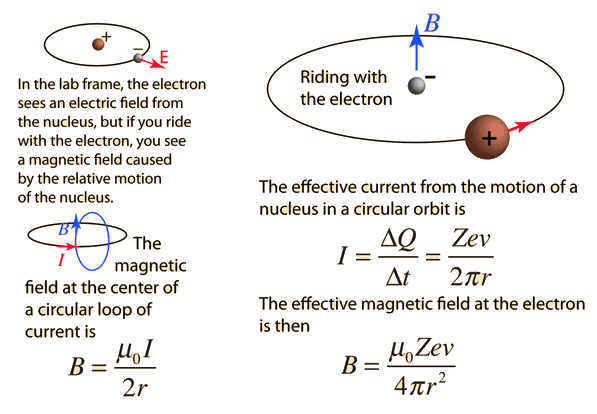
| The small splitting of the spectral line is attributed to an interaction between the electron spin S and the orbital angular momentum L. It is called the spin-orbit interaction. |
|
The familiar red H-alpha line of hydrogen is a single line according to the Bohr theory. The straight application of the Schrodinger equation to the hydrogen atom gives the same result. If you calculate the wavelength of this line using the energy expression from the Bohr theory, you get 656.11 nm for hydrogen, treating the nucleus as a fixed center. If you use the reduced mass, you get 656.47 nm for hydrogen and 656.29 nm for deuterium. The difference between the hydrogen and deuterium lines is about 0.2 nm and the splitting of each of them is about 0.016 nm, corresponding to an energy difference of about 0.000045 eV. This corresponds to an internal magnetic field on the electron of about 0.4 Tesla. |
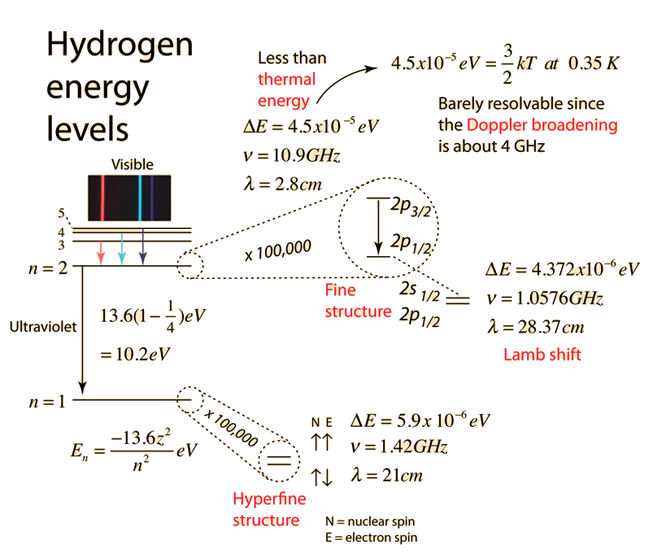
Active illustration: click for more detail
| Examination of fine structure by saturation spectroscopy |
Schrodinger equation concepts
Hydrogen concepts
Atomic structure concepts
Reference
Rohlf
Sec 8.6
| HyperPhysics***** Quantum Physics | R Nave |