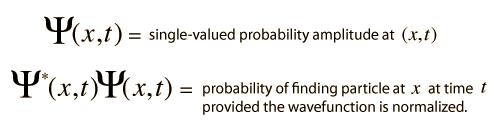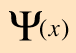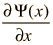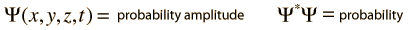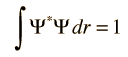Varieties of Wave Equations
Early in the 20th century, electrons were shown to have wave properties, and the wave-particle duality became a part of our understanding of nature. The mathematics for describing the behavior of such electron waves might be expected to be similar to that for describing classical waves, such as the wave on a stretched string
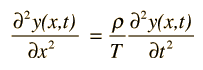
or a plane electromagnetic wave
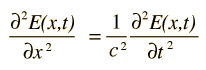
The wave equation developed by Erwin Schrodinger in 1926 shows some similarities in its one-dimensional form:
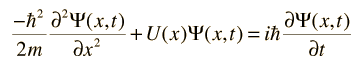
Schrodinger equation concepts
| HyperPhysics***** Quantum Physics | R Nave |