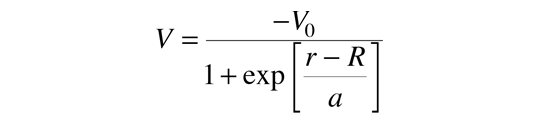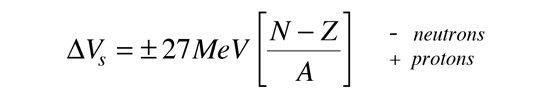Shell Model of Nucleus

Visualizing the densely packed nucleus in terms of orbits and shells seems much less plausible than the corresponding shell model for atomic electrons. You can easily believe that an atomic electron can complete many orbits without running into anything, but you expect protons and neutrons in a nucleus to be in a continuous process of collision with each other. But dense-gas type models of nuclei with multiple collisions between particles didn't fit the data, and remarkable patterns like the "magic numbers" in the stability of nuclei suggested the seemingly improbable shell structure.

With the enormous strong force acting between them and with so many nucleons to collide with, how can nucleons possibly complete whole orbits without interacting? This has the marks of a Pauli exclusion principle process, where two fermions cannot occupy the same quantum state. If there are no nearby, unfilled quantum states that are in reach of the available energy for an interaction, then the interaction will not occur. This is essentially a quantum idea - if there is not an available "hole" for a collision to knock a nucleon into, then the collision will not occur. There is no classical analog to this situation.

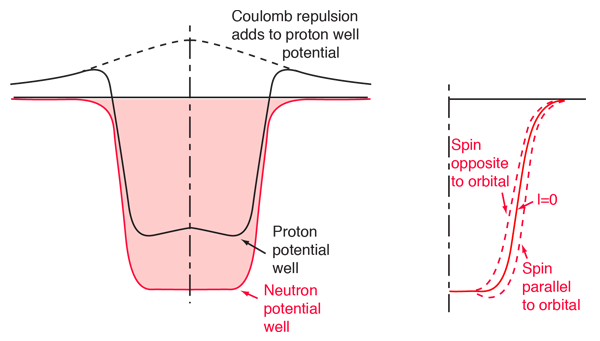
The evidence for a kind of shell structure and a limited number of allowed energy states suggests that a nucleon moves in some kind of effective potential well created by the forces of all the other nucleons. This leads to energy quantization in a manner similar to the square well and harmonic oscillator potentials. Since the details of the well determine the energies, much effort has gone into construction of potential wells for the modeling of the observed nuclear energy levels. Solving for the energies from such potentials gives a series of energy levels like that at left below. The labels on the levels are somewhat different from the corresponding symbols for atomic energy levels. The energy levels increase with orbital angular momentum quantum number l, and the s,p,d,f... symbols are used for l=0,1,2,3... just like the atomic case. But there is really no physical analog to the principal quantum number n, so the numbers associated with the level just start at n=1 for the lowest level associated with a given orbital quantum number, giving such symbols as 1g which could not occur in the atomic labeling scheme. The quantum number for orbital angular momentum is not limited to n as in the atomic case.

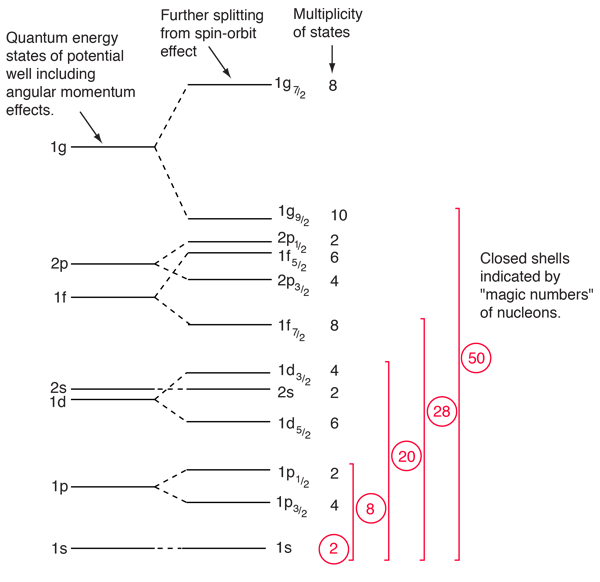
In addition to the dependence on the details of the potential well and the orbital quantum number, there is a sizable spin-orbit interaction which splits the levels by an amount which increases with orbital quantum number. This leads to the overlapping levels as shown in the illustration. The subscript indicates the value of the total angular momentum j, and the multiplicity of the state is 2j + 1. The contribution of a proton to the energy is somewhat different from that of a neutron because of the coulomb repulsion, but it makes little difference in the appearance of the set of energy levels.

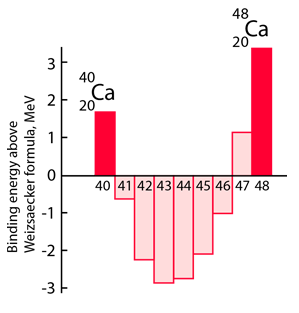
With this set of identified nuclear states and the magic numbers, we can predict the net nuclear spin of a nucleus and represent it's nuclear state based on the identification of the level of the odd nucleon in the order of states shown above. The parity of the state can also be predicted, so the single particle shell model has shown itself to be of significant benefit in characterizing nuclei.

"Magic Numbers" in Nuclear Structure

It is found that nuclei with even numbers of protons and neutrons are more stable than those with odd numbers. In particular, there are "magic numbers" of neutrons and protons which seem to be particularly favored in terms of nuclear stability:

2, 8, 20, 28, 50, 82, 126

Nuclei which have both neutron number and proton number equal to one of the magic numbers can be called "doubly magic", and are found to be particularly stable.

Calcium provides a good example of the exceptional stability of "doubly magic" nuclei since it has two of them. The existence of several stable isotopes of calcium may have to do with the fact that Z=20, a magic number. The two highlighted isotopes have neutron numbers 20 and 28, also magic numbers. Compared to the binding energy calculated from the Weizsaecker formula, they both have more than the expected binding energy.

The existence of these magic numbers suggests closed shell configurations, like the shells in atomic structure. They represent one line of reasoning which led to the development of a shell model of the nucleus. Other forms of evidence suggesting shell structure include the following.

1. Enhanced abundance of those elements for which Z or N is a magic number.
2. The stable elements at the end of the naturally occuring radioactive series all have a "magic number" of neutrons or protons.
3. The neutron absorption cross-sections for isotopes where N = magic number are much lower than surrounding isotopes.
4. The binding energy for the last neutron is a maximum for a magic neutron number and drops sharply for the next neutron added.
5. Electric quadrupole moments are near zero for magic number nuclei.
6. The excitation energy from the ground nuclear state to the first excited state is greater for closed shells.

Nuclear Potential and the Shell Model

The shell model of the nucleus presumes that a given nucleon moves in an effective attractive potential formed by all the other nucleons. If that is true, then the potential is probably roughly proportional to the nuclear density and therefore could be expressed in the form

The parameters in this model of the potential have been evaluated to be approximately:

Note that the radius above is larger than that given by the nuclear radius formula since it is related to the nuclear force which extends beyond the radius. Two other corrections are typically applied to more nearly fit observations. The first is called the symmetry energy, arising when there is an unequal number of protons and neutrons. Empirically, it is evaluated as

The other correction for protons is the electrostatic repulsion energy, which takes the form

The approximate potentials for neutrons and protons take the general form shown at left below.

The additional correction which must be made is the spin-orbit interaction. Its general effect on the potential well is shown in the sketch above right. If the spin is opposite to the orbital angular momentum, the effective potential well is narrower, giving higher energy in the same manner as the square well potential. This can be seen in the spin-orbit splittings in the shell model level diagram.