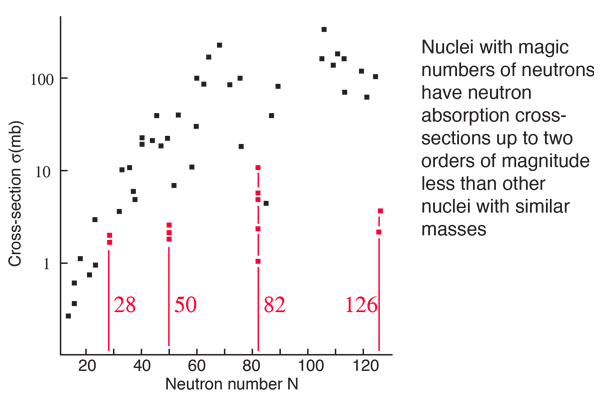
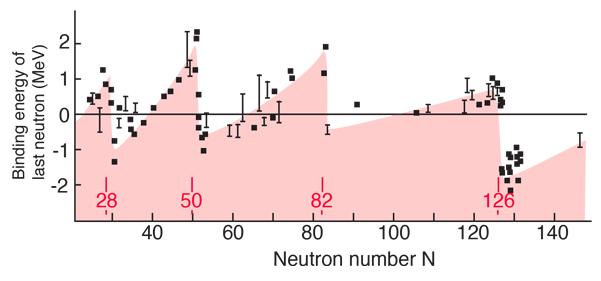
Enhanced Abundance of Magic Number Nuclei
Part of the motivation for the shell model of nuclear structure is the existance of "magic numbers" of neutrons and protons at which the nuclei have exceptional stability, implying some kind of "closed shell". One indication of this stability is the enhanced abundance of isotopes which have a magic number of neutrons or protons.
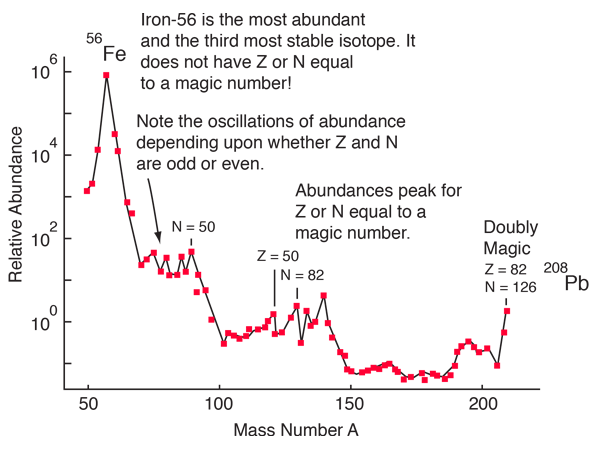
After Booth & Combley
The illustration examines the abundance of elements around iron and above. Our model of heavy element formation involves extraordinary processes in supernovae. Since these nuclei are born in the maelstrom of neutrons and neutrinos in the violent outer reaches of the supernovae, one would expect a statistical advantage for those isotopes which are most stable and therefore have the smallest cross-section for the kind of scattering which would disrupt them.
While the peaks in abundance for the magic number isotopes do not appear to be particularly prominent, keep in mind that the vertical scale is logaritmic.
The iron-56 is a particularly unique case, as shown by its extraordinary abundance. Iron-56 is an even-even nucleus and therefore expected to be particularly stable because of the Pauli contribution in the liquid drop model, but does not have magic numbers of either N or Z. It is exceeded in binding energy only by nickel-62 (the most stable nuclide) and iron-58. It is near the peak of the binding energy curve, and therefore can be considered to be one of the end points of both nuclear fusion and fission sequences, so perhaps that is the explanation for its extraordinary abundance.
| Evidence for nuclear shell structure | "Magic numbers" of nucleons |
Nuclear Structure Concepts
Reference
Booth & Combley
| HyperPhysics***** Nuclear | R Nave |