Spherical Potential Well
The idealized infinite-walled one-dimensional and three-dimensional square-well potentials can be solved by the Schrodinger equation to give quantized energy levels. For the case of a nucleus, a useful idealization is an infinite-walled spherical potential. That is, we model the nucleus with a potential which is zero inside the nuclear radius and infinite outside that radius.
In spherical polar coordinates, the Shrodinger equation is separable in the general form Ψ(r,θ,φ) = R(r)Θ(θ)Φ(φ), as it is in the case of the hydrogen atom solution. In this case with zero potential, the separation of the azimuthal (φ) and colatitude (θ) equations requires

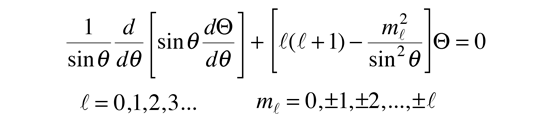
The solutions for Θ and Φ, when normalized, give a standard set of functions called spherical harmonics.
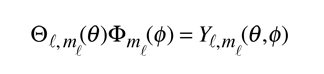
The radial equation is
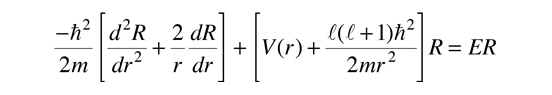
and the solution of this equation can be expressed in terms of another set of functions called spherical Bessel functions.
| "Magic numbers" of nucleons | Nuclear potential wells | Nuclear spectra |
Nuclear Structure Concepts
Reference
Krane
Ch 2
| HyperPhysics***** Nuclear | R Nave |