Nuclear Magnetic Moments
Associated with each nuclear spin is a magnetic moment which is associated with the angular momentum of the nucleus. It is common practice to express these magnetic moments in terms of the nuclear spin in a manner parallel to the treatment of the magnetic moments of electron spin and electron orbital angular momentum.
For the electron spin and orbital cases, the magnetic moments are expressed in terms of a unit called a Bohr magneton which arises naturally in the treatment of quantized angular momentum.

Generally, the measured quantity is proportional to the z-component of the magnetic moment (the component along the experimentally determined direction such as the direction of an applied magnetic field, etc. ). In this treatment, the use of a "gyromagnetic ratio" or "g-factor" is introduced. The g-factor for orbital is just gL = 1, but the electron spin g-factor is approximately gS = 2.
For the nuclear case we proceed in a parallel manner. The nuclear magnetic moment is expressed in terms of the nuclear spin in the form
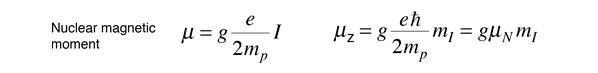
where we have now introduced a new unit called a nuclear magneton.
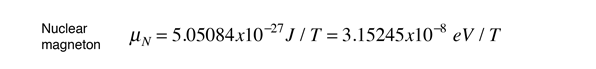
For free protons and neutrons with spin I =1/2, the magnetic moments are of the form
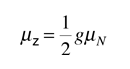
where
Proton: g = 5.5856947
In 2014 a direct measurement of the magnetic moment of the proton gave 2.792847350(9) nuclear magnetons. (Mooser et al, Nature, May 29, 2014). Efforts are underway to measure the magnetic moment of the antiproton with comparable accuracy, since a measured difference between the proton and antiproton could be a valuable clue toward unraveling the mystery of why matter greatly dominates antimatter in the universe (antimatter problem).
Neutron: g = -3.8260837 +/- 0.0000018
The proton g-factor is far from the gS = 2 for the electron, and even the uncharged neutron has a sizable magnetic moment! For the neutron, this suggests that there is internal structure involving the movement of charged particles, even though the net charge of the neutron is zero. If g=2 were an expected value for the proton and g=0 were expected for the neutron, then it was noted by early researchers that the the proton g-factor is 3.6 units above its expected value and the neutron value is 3.8 units below its expected value. This approximate symmetry was used in trial models of the magnetic moment, and in retrospect is taken as an indication of the internal structure of quarks in the standard model of the proton and neutron.
Note that the maximum effective magnetic moment of a nucleus in nuclear magnetons will be the g-factor multiplied by the nuclear spin. For a proton with g = 5.5857 the quoted magnetic moment is μ = 2.7928 nuclear magnetons.
| Nuclide | spin I | μ in μN |
| -1.9130418 | ||
| +2.7928456 | ||
| +0.8574376 | ||
| -1.89279 | ||
| +0.09062293 | ||
| +4.733 | ||
| +6.1705 |
Data from V. S. Shirley, Table of Isotopes, Wiley, New York, 1978, Appendix VII.
| Nuclear magnetic resonance |
Nuclear Structure Concepts
Reference
Krane
Ch 3
| HyperPhysics***** Nuclear | R Nave |