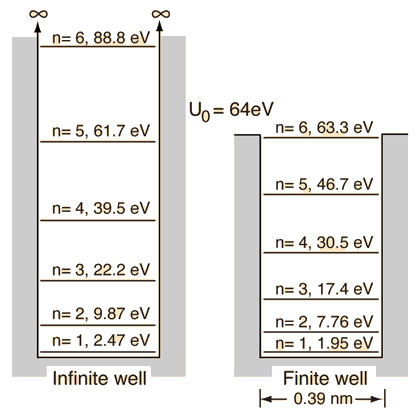
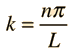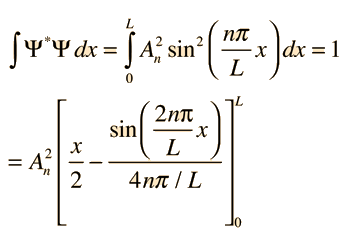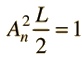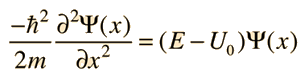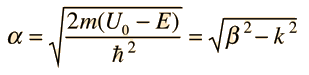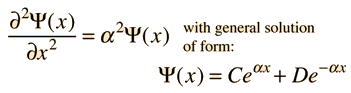Particle in a Box
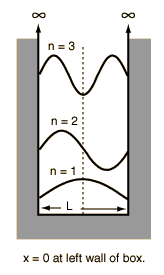 |
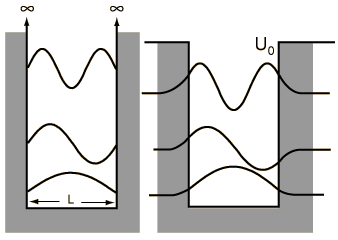
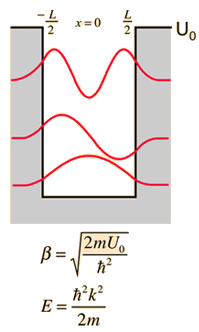
Assume the potential U(x) in the time-independent Schrodinger equation to be zero inside a one-dimensional box of length L and infinite outside the box. For a particle inside the box a free particle wavefunction is appropriate, but since the probability of finding the particle outside the box is zero, the wavefunction must go to zero at the walls. This constrains the form of the solution to 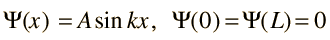
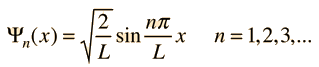 |
| Discussion of significance | Quantized energies | Containment energies | Finite-walled box |
| 3-D particle in box |
Schrodinger equation concepts
| HyperPhysics***** Quantum Physics | R Nave |