Un Buen Absorbente es un Buen Emisor

De acuerdo con la ley de Stefan-Boltzmann, la energía radiada por un radiador de cuerpo negro por segundo y por unidad de área, es proporcional a la cuarta potencia de la temperatura absoluta y está dada por

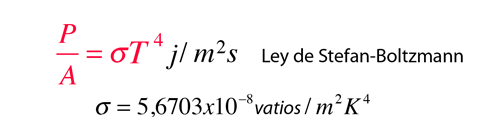
Para objetos calientes distintos de los radiadores ideales, la ley se expresa en la forma

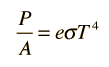
donde e es la emisividad del objeto (e = 1 para un radiador ideal). Si el objeto caliente está radiando energía hacia su mas frío entorno, que está a una temperatura T_c, la tasa de pérdida por radiación neta, toma la forma

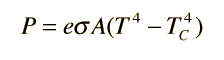
En esta fórmula, el término con T_c representa la energía absorbida del entorno. Esta expresión asume explícitamente que se aplica el mismo coeficiente e a ambos, la emisión sobre el entorno y la absorción del mismo. Es decir, un buen emisor es un buen absorbente y viceversa; se puede usar el mismo coeficiente para representar ambos procesos. ¿Por que es esto verdad?

Quizás la manera más conceptual y fundamental de abordar esta cuestión sea observar que un objeto caliente colocado en una habitación, en última instancia deberá llegar a un equilibrio térmico con el ambiente. El objeto caliente inicialmente emiten más energía a la sala de lo que absorbe de la misma, pero hará que la temperatura de la habitación suba y la temperatura del objeto caiga. Pero cuando llegan a la misma temperatura, se puede concluir que la cantidad de energía absorbida en promedio, es exactamente la misma que la energía emitida. Es decir, la expresión anterior para la energía neta irradiada con el medio ambiente, nos debe dar cero cuando T=T_c.

El argumento anterior se basa en la segunda ley de la termodinámica en la forma que establece que, el calor no fluirá espontáneamente desde un objeto frío hacia uno mas caliente. Si el coeficiente de absorción fuera mayor que el coeficiente de emisión del objeto, entonces podría absorber energía neta de la habitación, incluso aunque su temperatura fuera mas alta que la de la habitación.

Pero supongamos que quisiéramos argumentar que un buen absorbente debe ser un buen emisor, basándonos en los procesos microscópicos donde participan los átomos de la superficie de un objeto. Entonces se convierte en una cuestión cuántica, que implica las siguientes ideas:

1. Toda radiación electromagnética, se puede considerar cuantizada. Esta radiación existe en forma de fotones que tienen una energía dada por la hipótesis de Planck, E=hf.

2. Para que un sólido (o cualquiera otra materia, pero estoy asumiendo que hablamos de sólidos) pueda absorber un fotón de una energía dada hf, debe tener un par de niveles de energía separado por esa cantidad hf, de modo que el fotón eleva el sistema, desde el miembro inferior del par al superior.

3. En la luz visible o cerca de la visible, los pares de niveles de energía que participan en la mayoría de las absorciones, son niveles de energía de electrones, de modo que cuando se absorbe un fotón verde con energía de fotón de 2,2 eV., hace que un electrón muy cerca de la superficie del sólido, salte hacia arriba hacia un desnivel por encima de 2,2 eV. No podrá hacerlo al menos que haya un desnivel de 2,2 eV. para recibirlo.

4. Si la superficie es un absorbente ideal en el visible, resulta que hay una gran cantidad de estados electrónicos disponibles, para que un fotón de cualquier color en el espectro visible, pueda interactuar con los electrones en el sólido y elevarlos a un nivel superior disponible. La implicación es que cualquier color en el espectro visible puede ser absorbido fácilmente, por lo que se trata de un absorbente ideal, un objeto perfectamente negro.

5. El siguiente paso no es tan obvio. Si un par de niveles de energía de electrón está disponible para la absorción de un fotón, tambien estará disponible para la emisión de un fotón, por ejemplo por radiación. Si está disponible para un salto hacia arriba, también lo estará para un salto hacia abajo. Una de las contribuciones de Einstein fue demostrar que para una determinada radiación, la probabilidad de emisión es la misma que la probabilidad de radiación. Este hecho se describe en términos de los coeficientes A y B de Einstein y es muy importante en la teoría laser. La implicación ahora en este asunto es ¿qué limita a un buen absorbente ser un buen emisor?. Si el sólido tiene un montón de niveles electrónicos disponibles para la absorción, tambien estarán igualmente disponibles para la radiación. Para cerrar el círculo del debate, Einstein primero dedujo sus coeficientes A y B de un argumento termodinámico como el argumento de arriba sobre el equilibrio térmico, antes del desarrollo actual de las ideas mecánicas cuánticas.

La conclusión de este razonamiento es que un buen absorbente de la radiación también será un buen emisor. Pero lo anterior es sólo la punta del iceberg. En un objeto negro, todos los colores visibles se absorben por saltos electrónicos, pero los electrones elevados a esos niveles, siguen normalmente un camino hacia abajo diferente, realizando una cascada de saltos mas pequeños hacia abajo, asociados quizás con la radiación infrarroja. De modo que decimos que el objeto absorbe la luz y se calienta, asociando el calor con el rango infrarrojo del espectro electromagnético. Sin embargo, es un buen emisor, solo que toma la luz como visible y la irradia como infrarroja. En este radiador en equilibrio, la fracción de luz que emite en cualquier rango de longitud de onda depende de la temperatura, y en un radiador ideal se distribuye en longitudes de onda de acuerdo con la fórmula del cuerpo negro. La gran complejidad de tratar con todos los mecanismos y procesos cuánticos en un sólido, es el tipo de cosas que podría haber llevado supuestamente a Einstein, a su preferencia siempre que era posible, de abordar los problemas desde una perspectiva termodinámica.