Oscilador Armónico Cuántico: Funciones de Onda
Se puede resolver la ecuación de Schrodinger de un oscilador armónico, para dar las funciones de onda ilustradas abajo.
| Comparación de las Probabilidades Clásicas y Cuánticas |
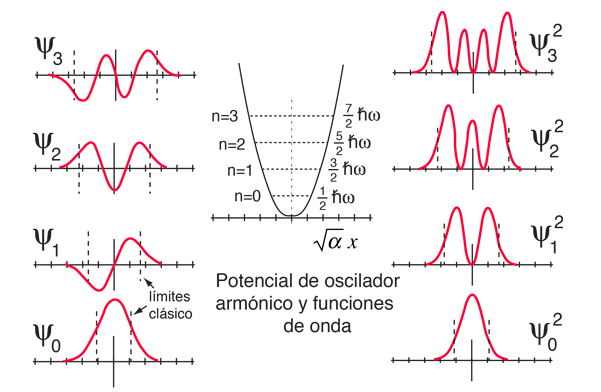
 | La solución de la ecuación de Shrodinger para los primeros cuatro estados de energía, da las funciones de onda normalizadas de la izquierda. Estas funciones se representan a la izquierda en la ilustración de arriba. La probabilidad de encontrar el oscilador en cualquier valor dado de x, es el cuadrado de la función de onda, y esos cuadrados se muestran arriba a la derecha. Nótese que las funciones de onda para un mayor n, tienen más "jorobas" en el pozo de potencial. Esto corresponde a una longitud de onda más corta, y por lo tanto por la fórmula de DeBroglie, se puede ver que tienen un momento más alto, y por lo tanto más alta energía. El valor más probable de la posición para los estados inferiores es muy diferente del oscilador armónico clásico, donde pasa más tiempo cerca de los extremos de su movimiento. Pero a medida que aumenta el número cuántico, la distribución de probabilidad se parece más a la del oscilador clásico -esta tendencia de acercarse al comportamiento clásico en los números cuánticos altos, se llama principio de correspondencia-. |
 | Cuando la ecuación de Schrödinger para el oscilador armónico se resuelve mediante el método de series, las soluciones contienen este conjunto de polinomios, llamado polinomios de Hermite. |
Las funciones de onda del oscilador armónico cuántico, contienen la forma gaussiana que les permite satisfacer las condiciones de contorno necesarias en el infinito. En la función de onda asociada con un valor dado del número cuántico n, el gaussiano es multiplicado por un polinomio de orden n, (los polinomios de Hermite de arriba), y las constantes necesarias para normalizar las funciones de onda.
Conceptos de la Ecuación de Schrödinger
Referencias
Beiser, Perspectives
Sec 8-7
Thornton & Rex
Sec 7-6
| HyperPhysics*****Física Cuántica | M Olmo R Nave |