El Principio de Correspondencia y el Oscilador Cuántico

La mecánica cuántica es necesaria para la descripción de la naturaleza a escala atómica, pero las leyes de Newton van bien para pelotas de béisbol. En algún lugar a lo largo del continuo que va desde la cuántica a la clásica, las dos descripciones deben fusionarse. Empezando desde el final cuántico, y teniendo en cuenta que las energías dependen de un número cuántico, se podría prever que con números cuánticos suficientemente altos, el tratamiento cuántico debe fusionarse con el clásico. Esta idea de la fusión de la cuántica y la clásica se conoce como el "principio de correspondencia".

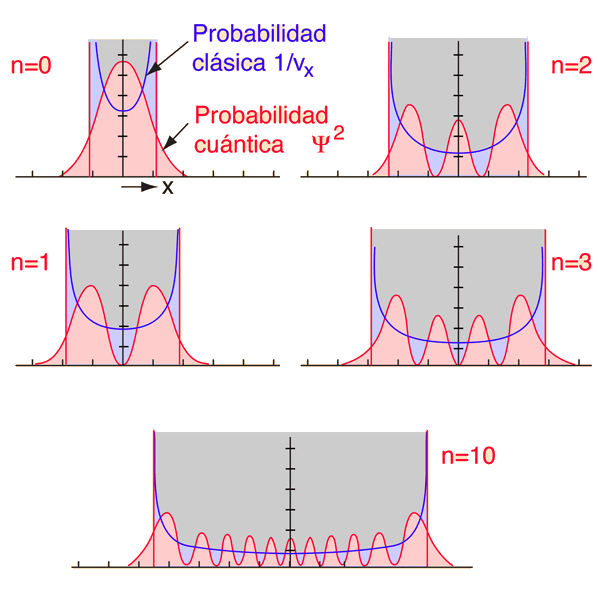
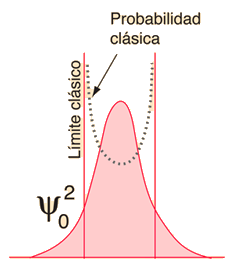Si se examina el estado fundamental del oscilador armónico cuántico, el principio de correspondencia parece poco probable, ya que las predicciones clásica y cuántica de la ubicación más probable están en total contradicción. Si se toma la posición de equilibrio del oscilador en x=0, entonces el oscilador cuántico predice que para el estado fundamental, el oscilador se pasa la mayor parte de su tiempo cerca de ese punto central. La masa-sobre-un-muelle clásica, obviamente, pasa muy poco tiempo allí, porque es donde tiene la velocidad máxima, pasando la mayor parte de su tiempo cerca de los puntos extremos de su oscilación, donde su velocidad es pequeña.

A medida que se avanza hacia estados más altos de la oscilación cuántica mediante el aumento de n, la ubicación más probable se desplaza hacia el exterior del pozo. Aún se dispone de la onda de probabilidad, que es característica de la solución de onda, pero al menos, la tendencia general de la probabilidad cuántica empieza a parecerse más a la probabilidad clásica que se muestra por la línea de trazos.
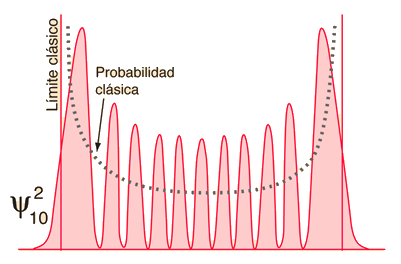Esta oscilación salvaje de la probabilidad, tiene sólo consecuencias prácticas si es observable, y cuanto mayor es el número cuántico, menor es la distancia entre los picos. Con n suficientemente alto, el principio de incertidumbre, impide resolver los huecos entre picos sin alterar el estado físico del oscilador. Las colas exponenciales en la región prohibida clásicamente, disminuyen al aumentar n, por lo que el oscilador cuántico se va viendo más y más como uno clásico.

Bohr utilizó el término "principio de correspondencia" y esperaba que el comportamiento radiativo de los átomos, se acercarían a la radiación clásica por cargas aceleradas, para estados cuánticos suficientemente altos. Ciertamente, las líneas espectrales observadas de los átomos, difieren radicalmente del comportamiento clásico. Beiser da un ejemplo del cálculo de la frecuencia de radiación de un átomo de número cuántico n=10.000 y declara que difiere del resultado clásico por sólo el 0,01%.

Mayor Detalle sobre las Probabilidades Clásicas y Cuánticas
 Índice

Conceptos de la Ecuación de Schrödinger

Referencias
Beiser, Perspectives
Sec 6-6
Thornton & Rex
Sec 7-6, 8-7
 
HyperPhysics*****Física CuánticaM Olmo R Nave
 Atrás





Comparación de Probabilidades Clásica y Cuántica del Oscilador Armónico

El oscilador armónico es un problema importante tanto en el dominio cuántico, como clásico. También es un buen ejemplo de cuan diferentes pueden ser los resultados cuánticos y clásicos. Un tipo de comparación es el de la probabilidad de encontrar un objeto que está oscilando, a una distancia x dada desde la posición de equilibrio. Para el caso clásico, la probabilidad es mayor hacia los extremos del movimiento, en donde se mueve más lentamente, llegando a parar instantáneamente en los extremos del movimiento. La probabilidad relativa de encontrarlo en cualquier intervalo Dx, es simplemente la inversa de su velocidad media en ese intervalo. Para el caso de la mecánica cuántica, la probabilidad de encontrar el oscilador en un intervalo Dx es el cuadrado de la función de onda, y esto resulta muy diferente para los estados más bajos de energía. Nótese en el diagrama para el estado fundamental (n=0) de abajo, que la probabilidad máxima está en el punto de equilibrio x=0.

Durante los primeros pocos niveles de energía cuántica, se puede ver muy poco parecido entre las probabilidades cuánticas y clásicas, pero cuando se llega al valor n=10 empieza a haber alguna similitud. Desde luego, no tienen el mismo aspecto, pero sí coinciden en que la probabilidad es mayor cerca de los extremos del movimiento. A medida que se avanza a valores muy altos de n, se vuelven más y más parecidas, y las oscilaciones de la probabilidad cuántica están tan próximas entre sí, que están prácticamente juntas. El hecho de que el resultado general de la probabilidad de encontrar el oscilador en un valor determinado de x, converja para los panoramas cuántico y clásico, se llama principio de correspondencia.

Otra cosa a tener en cuenta sobre las probabilidades clásicas y cuánticas de arriba, es que la probabilidad clásica está estrictamente contenida entre las líneas verticales que representan el límite clásico. Las probabilidades cuánticas se extienden dentro de la región clásicamente prohibida, decayendo exponencialmente en esa región.

Probabilidades Superpuestas sobre el Potencial de Oscilador
Índice

Conceptos de la Ecuación de Schrödinger

Referencia
Blatt
Cap. 7
 
HyperPhysics*****Física CuánticaM Olmo R Nave
 Atrás