Cualquier punto P puede ser representado por tres números con signo, generalmente escritos (x, y, z), donde la coordenada es la distancia perpendicular desde el plano formado por los otros dos ejes.
A menudo las posiciones son especificados por un vector de posición r que se puede expresar en términos de los valores de coordenadas y de vectores unitarios.
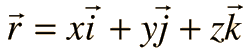
Aunque el sistema de coordenadas entero se puede girar, las relaciones entre los ejes debe fijarse de acuerdo con la regla de la mano derecha para el sistema de coordenadas.
La distancia entre dos puntos en coordenadas rectangular, se puede calcular por medio de las relaciones de distancia
|