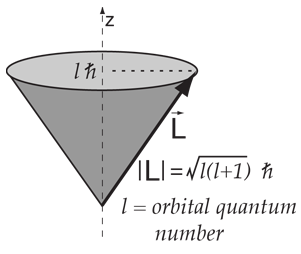
Angular Momentum in a Magnetic Field
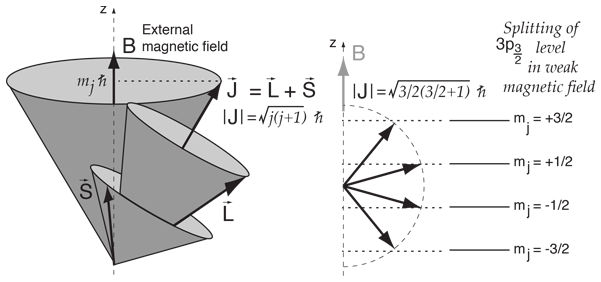
Once you have combined orbital and spin angular momenta according to the vector model, the resulting total angular momentum can be visuallized as precessing about any externally applied magnetic field.
This is a useful model for dealing with interactions such as the Zeeman effect in sodium. The magnetic energy contribution is proportional to the component of total angular momentum along the direction of the magnetic field, which is usually defined as the z-direction.
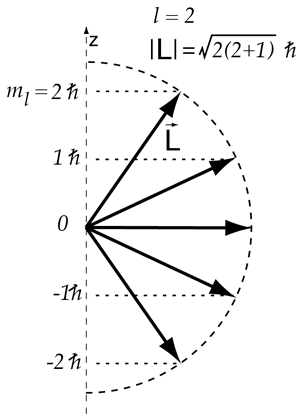
The z-component of angular momentum is quantized in values one unit apart, so for the upper level of the sodium doublet with j=3/2, the vector model gives the splitting shown.
Even with the vector model, the determination of the magnitude of the Zeeman spliting is not trivial since the directions of S and L ar constantly changing as they precess about J. This problem is handled with the Lande' g-factor.
This treatment of the angular momentum is appropriate for weak external magnetic fields where the coupling between the spin and orbital angular momenta can be presumed to be stronger than the coupling to the external field. This can be visualized with the help of a vector model of total angular momentum. If the external field is very strong, then it can decouple the spin and orbital angular momenta. This strong field case is called the Paschen-Back effect and leads to different patterns of splitting of the energy levels.
|