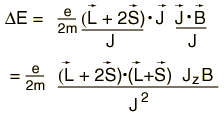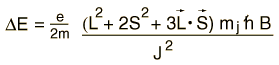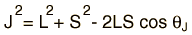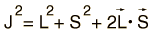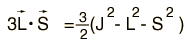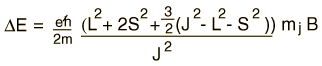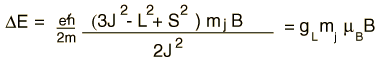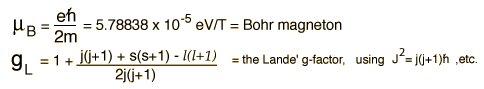Magnetic Interactions and the
Lande' g-Factor

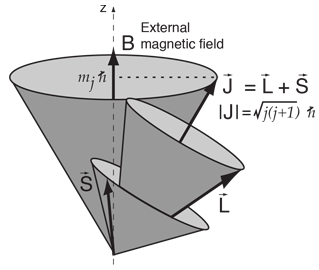
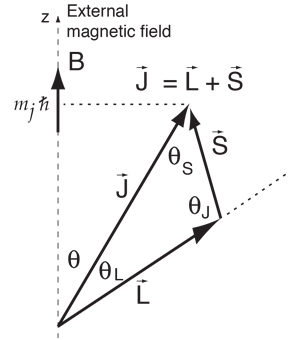
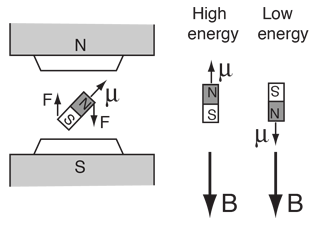A magnetic moment experiences a torque in a magnetic field B. The energy of the interaction can be expressed as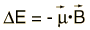

Both the orbital and spin angular momenta contribute to the magnetic moment of an atomic electron.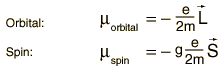

.
where g is the spin g-factor and has a value of about 2, implying that the spin angular momentum is twice as effective in producing a magnetic moment.

The interaction energy of an atomic electron can then be written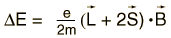

which when evaluated in terms of the relevant quantum numbers takes the form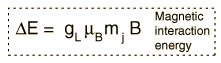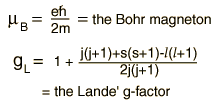

Show evaluation process

Zeeman interaction

Anomalous Zeeman effect

Index

Schrodinger equation concepts

Hydrogen concepts

HyperPhysics***** Quantum Physics

R Nave

Go Back

Evaluating the Lande' g-Factor

The Lande' g-factor is a geometric factor which arises in the evaluation of the magnetic interaction which gives the Zeeman effect. The magnetic interaction energy

which is continuous in the classical case takes on the quantum form

which is like a vector operation based on the vector model of angular momentum

The problem with evaluating this scalar product is that L and S continually change in direction as shown in the vector model. The strategy for dealing with this problem is to use the direction of the total angular momentum J as a coordinate axis and obtain the projection of each of the vectors in that direction. This is done by taking the scalar product of each vector with a unit vector in the J direction.

These vector relationships must be evaluated and expressed in terms of quantum numbers in order to evaluate the energy shifts. Carrying out the scalar products above leads to