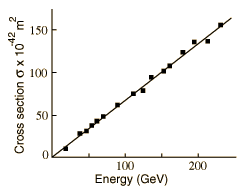
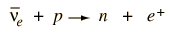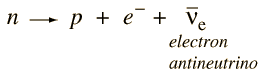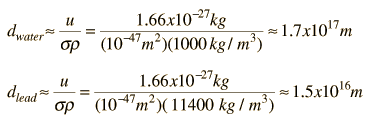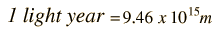Left-Handed Neutrinos
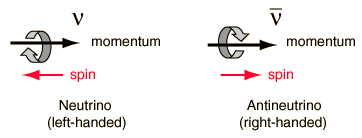
The relative orientations of spin and linear momentum for neutrinos and antineutrinos is apparently fixed and intrinsic to the particles.
This property is related to the concept of parity and to the conservation laws which apply to particle interactions.
For neutrinos the spin is always opposite the linear momentum and this is referred to as "left-handed", whereas the antineutrinos are always "right-handed". This evokes the picture of the right-hand rule for vector angular momentum. In this convention, the fingers of the right hand are used to indicate the sense of the spin or orbital motion, with the thumb pointing in the direction of the defined angular momentum. The momentum of the particle is used to define a preferred direction in space, and if you curled the fingers of your right hand to show the sense of the "spin" of the antineutrino, your thumb would point in this momentum direction. Hence it is a "right-handed" particle. For the neutrino, you would have to use the fingers of your left hand to get your thumb to point in the direction of the linear momentum.
Prior to 1956 all the available experimental evidence suggested that "left-handed" vs "right-handed" was not a meaningful characterization of particle interactions since the laws of physics appeared to conserve parity. Interactions which proceed by the strong and electromagnetic were shown by experiment to "conserve parity". But the theoretical work of Lee and Yang and the experiment with cobalt-60 decay by Wu showed that this decay by the weak interaction did not conserve parity. This causes the weak interactions which emit neutrinos or antineutrinos to violate conservation of parity.
The property which has been called left-handed and right-handed here is called "helicity". The helicity of a particle is defined as the ratio ms/s, or the z-component of spin divided by the magnitude of the spin. By this definition in this case, the helicity is +1 for a right-handed antineutrino and -1 for a left-handed neutrino.
| Neutrinos as leptons | Role in supernova | Other neutrino types |
Reference
Griffiths, 2nd Ed
Sec 4.4
| HyperPhysics***** Quantum Physics | R Nave |