Rotation Vectors
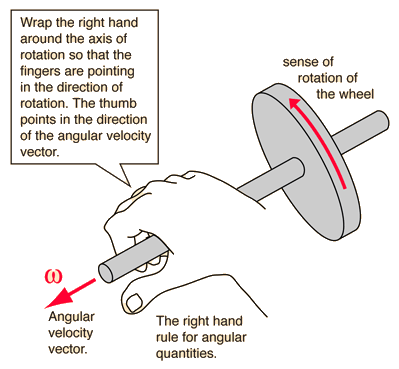 |
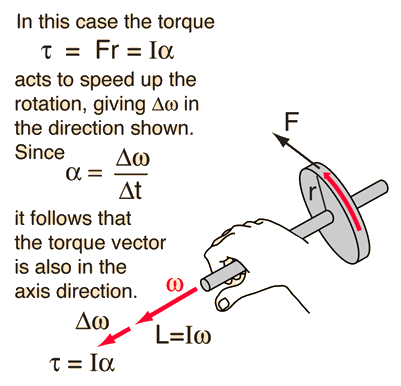
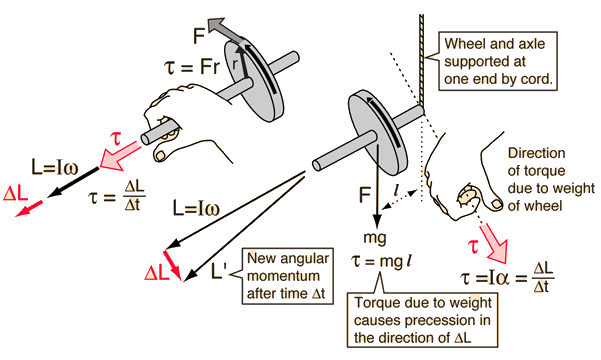
Angular motion has direction associated with it and is inherently a vector process. But a point on a rotating wheel is continuously changing direction and it is inconvenient to track that direction. The only fixed, unique direction for a rotating wheel is the axis of rotation, so it is logical to choose this axis direction as the direction of the angular velocity. Left with two choices about direction, it is customary to use the right hand rule to specify the direction of angular quantities.
|
| HyperPhysics***** Mechanics ***** Rotation | R Nave |