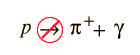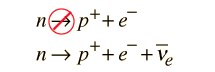Crossing Symmetry
If a particle interaction
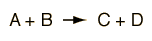
is observed to occur, then related interactions can be anticipated from the fact that any of the particles can be replaced by its antiparticle on the other side of the interaction. This is commonly known as "crossing symmetry". The observation of the above interaction implies the existence of the following interactions.
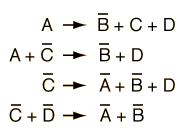
The overbar indicates the antiparticle. Crossing symmetry applies to all known particles, including the photon which is its own antiparticle. One example of the crossing principle is that of the relation between Compton scattering and electron-positron annihilation.
| Show in Feynman diagrams |
By examination, it can be seen that these two interactions are related by crossing symmetry. It could then be said that the observation of Compton scattering implies the existence of pair annihilation and predicts that it will produce a pair of photons.
Another example of crossing symmetry may have led Reines and Cowan to their experiment for the detection of the neutrino. If you take the electron product from the neutron decay reaction to the other side and convert it into a positron, then you have the reaction which they used.
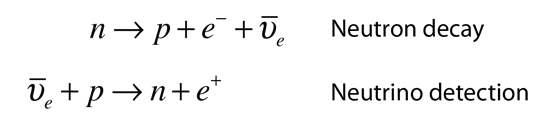
Particle concepts
Particle conservation laws
References
Griffiths
Ch. 2
| HyperPhysics***** Quantum Physics | R Nave |