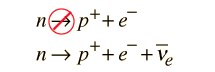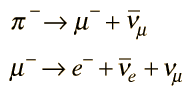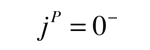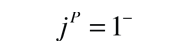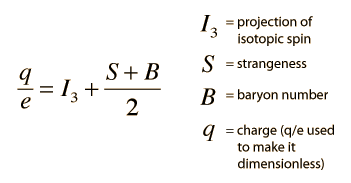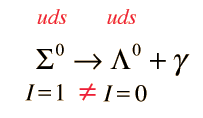Conservation of Baryon Number
Nature has specific rules for particle interactions and decays, and these rules have been summarized in terms of conservation laws. One of the most important of these is the conservation of baryon number. Each of the baryons is assigned a baryon number B=1. This can be considered to be equivalent to assigning each quark a baryon number of 1/3. This implies that the mesons, with one quark and one antiquark, have a baryon number B=0. No known decay process or interaction in nature changes the net baryon number.
The neutron and all heavier baryons decay directly to protons or eventually form protons, the proton being the least massive baryon. This implies that the proton has nowhere to go without violating the conservation of baryon number, so if the conservation of baryon number holds exactly, the proton is completely stable against decay. One prediction of grand unification of forces is that the proton would have the possibility of decay, so that possibility is being investigated experimentally.
Conservation of baryon number prohibits a decay of the type
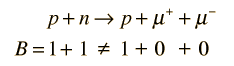
but with sufficient energy permits pair production in the reaction
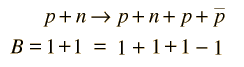
The fact that the decay
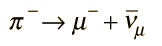
is observed implied that there is no corresponding principle of conservation of meson number. The pion is a meson composed of a quark and an antiquark, and on the right side of the equation there are only leptons. (Equivalently, you could assign a baryon number of 0 to the meson.)
Particle concepts
| HyperPhysics***** Quantum Physics | R Nave |