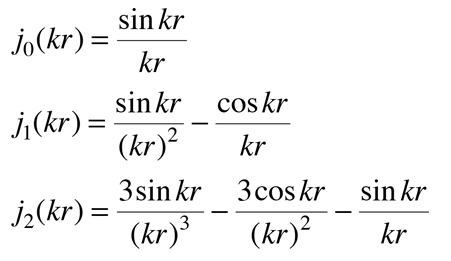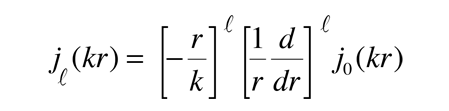Bessel Functions
One of the varieties of special functions which are encountered in the solution of physical problems is the class of functions called Bessel functions. They are solutions to a very important differential equation, the Bessel equation:
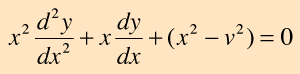
The solutions to this equation are in the form of infinite series which are called Bessel funtions of the first kind. The expression for the sum is
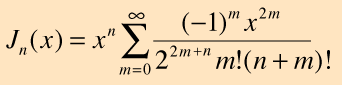
Values for the Bessel functions can be found in most collections of mathematical tables. Bessel functions are encountered in physical situations where there is cylindrical symmetry. This occurs in problems involving electric fields, vibrations, heat conduction, optical diffraction and others.
For the specific application to a spherical potential well in quantum mechanics, another form called spherical bessel functions appears.
Reference
Kreyszig
Sec 4.5
| HyperPhysics*****HyperMath*****Calculus | R Nave |