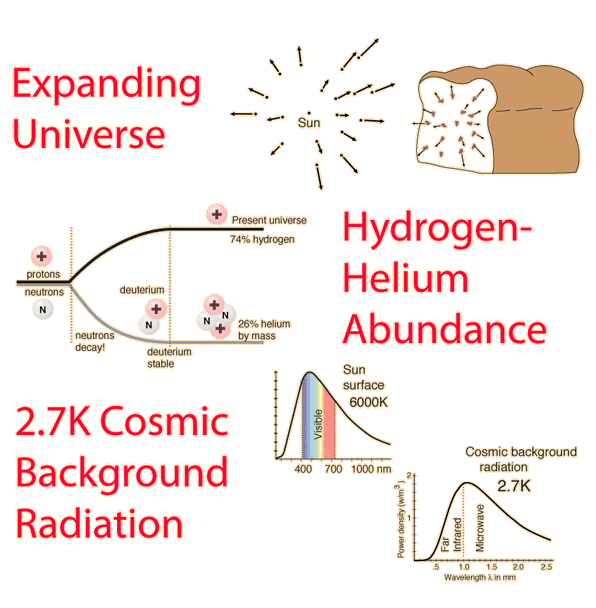
The Flatness Problem
Observations indicate that the amount of matter in the universe is surely greater than one-tenth and surely less than ten times the critical amount needed to stop the expansion. It is either barely open or barely closed, or "very nearly flat".
There is a good analogy here - a ball thrown up from the earth slows down. With the same velocity from a small asteroid, it might never stop (Trefil pp46-47). Early in this theoretical toss from the asteroid, it might appear that you have thrown it with just the right velocity to go on forever, slowing toward zero velocity at infinite time and distance. But as time progressed, it would become more and more evident if you had missed the velocity window even a small amount. If after 20 billion years of travel, it still appeared that you had thrown it with the right velocity, then that original throw was precise indeed.
Any departures from "flatness" should become exaggerated with time, and at this stage of the universe, tiny irregularities should have been much amplified. If the density of the present universe appears to be very close to the critical density, then it must have been even closer to "flat" in earlier epochs. Alan Guth credits a lecture by Robert Dicke as one influence which put him on the "inflationary" path; Dicke pointed out that the flatness of todays universe would require that the universe be flat to one part in 1014 at one second after the big bang. Kaufmann suggests that right after the big bang, the density must have been equal to the critical density to 50 decimal places!
In the early 1980's, Alan Guth proposed that there was a brief period of extremely rapid expansion following the Planck time of 10-43 seconds. This "inflationary model" was a way of dealing with both the flatness problem and the horizon problem. If the universe inflated by 20 to 30 orders of magnitude, then the properties of an extremely tiny volume which could have been considered to be intimately connected were spread over the whole of the known universe today, contributing both extreme flatness and the extremely isotropic nature of the cosmic background radiation.
|
Index
Reference
Trefil
Guth
Kaufmann
Ch. 29 |