Nuclear Binding Energy
Nuclei are made up of protons and neutrons, but the mass of a nucleus is always less than the sum of the individual masses of the protons and neutrons which constitute it. The difference is a measure of the nuclear binding energy which holds the nucleus together. This binding energy can be calculated from the Einstein relationship:
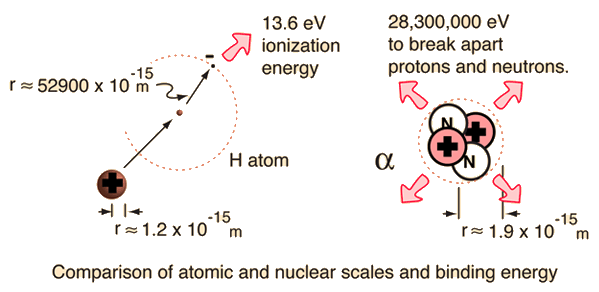
For the alpha particle Δm= 0.0304 u which gives a binding energy of 28.3 MeV.
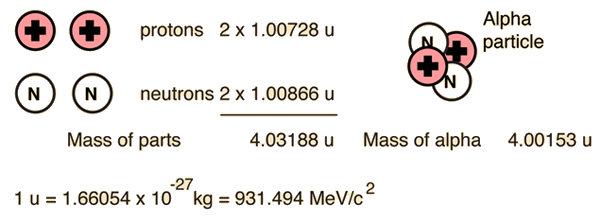
The enormity of the nuclear binding energy can perhaps be better appreciated by comparing it to the binding energy of an electron in an atom. The comparison of the alpha particle binding energy with the binding energy of the electron in a hydrogen atom is shown below. The nuclear binding energies are on the order of a million times greater than the electron binding energies of atoms.
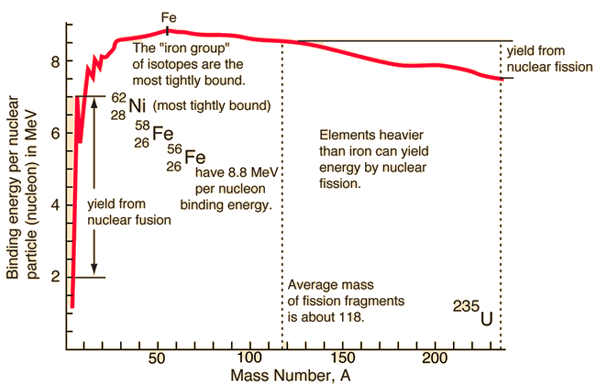
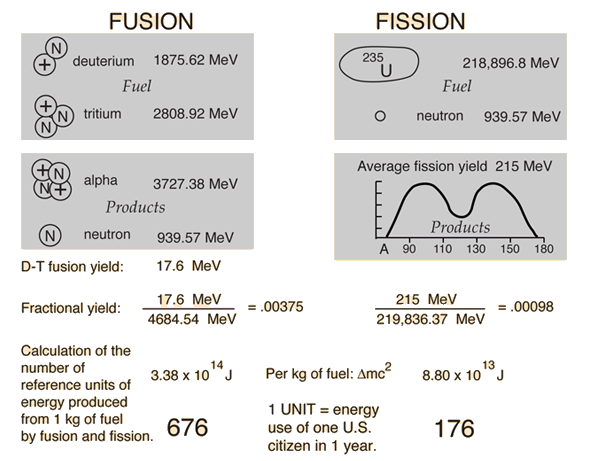
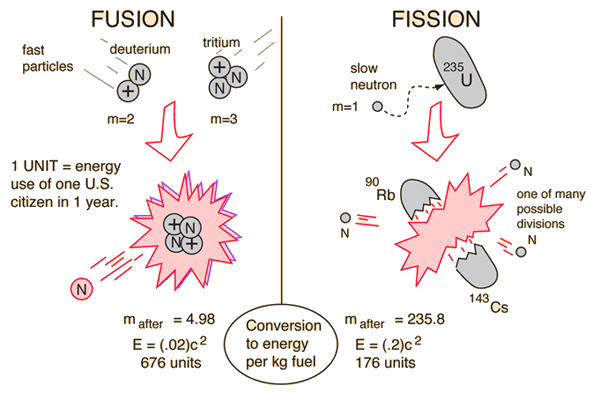
| Binding energy curve. | Nuclear units. |
Nuclear Structure Concepts
| HyperPhysics***** Nuclear | R Nave |