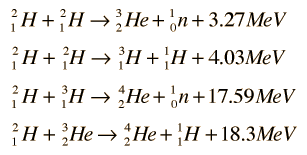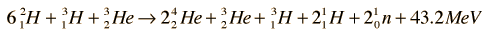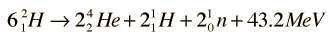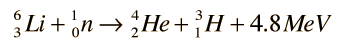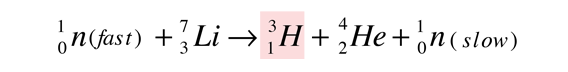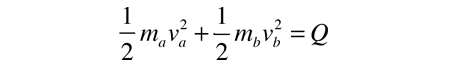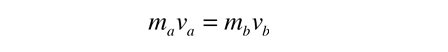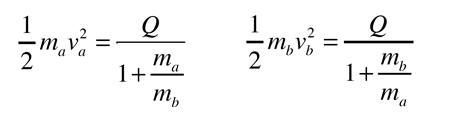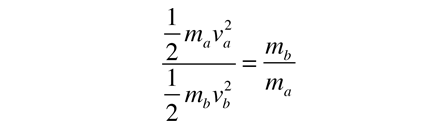Nuclear Fusion

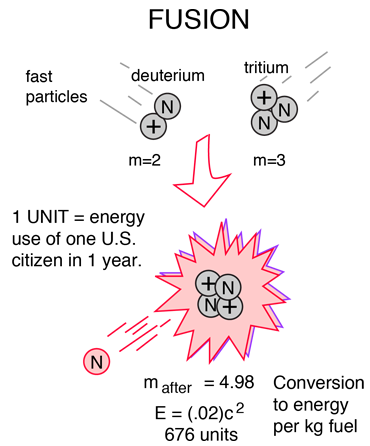
If light nuclei are forced together, they will fuse with a yield of energy because the mass of the combination will be less than the sum of the masses of the original individual nuclei. If the combined nuclear mass is less than that of iron at the peak of the binding energy curve, then the nuclear particles will be more tightly bound than they were in the lighter nuclei, and that decrease in mass comes off in the form of energy according to the Einstein relationship. For elements heavier than iron, fission will yield energy.

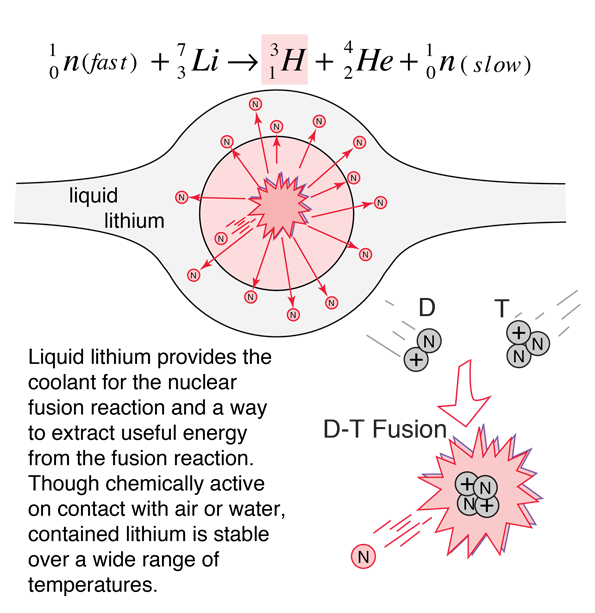
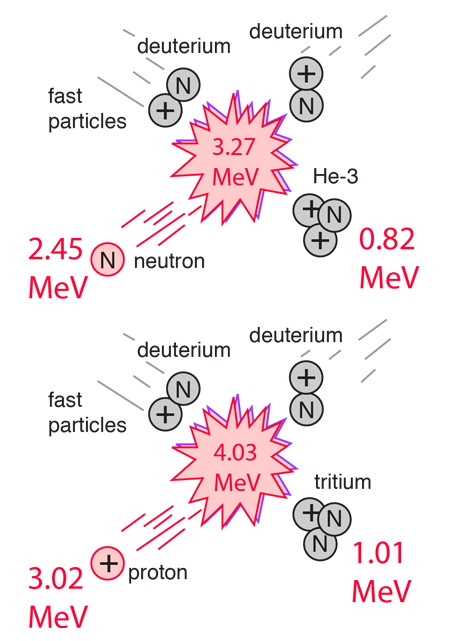
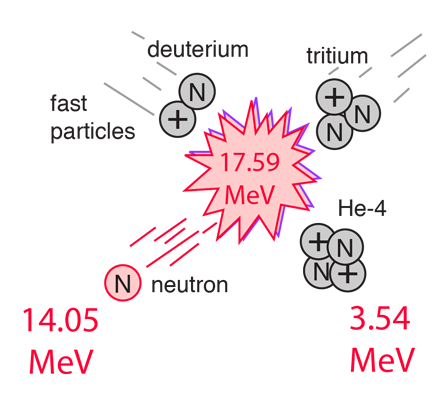
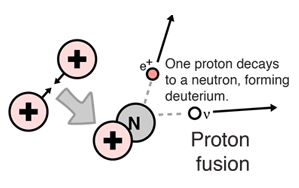
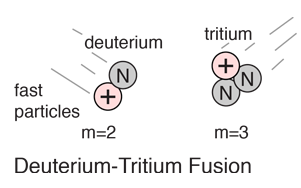
For potential nuclear energy sources for the Earth, the deuterium-tritium fusion reaction contained by some kind of magnetic confinement seems the most likely path. However, for the fueling of the stars, other fusion reactions will dominate.

The energy analysis of a nuclear fusion event involves evaluating the masses before and after it and taking the difference. The decrease in mass used in the Einstein relationship represents the energy yield Q.

Using deuterium fusion with a neutron yield as an example, it is typical to use the units GeV/c² to represent the masses of the constituents. In those units the above fusion reaction becomes

The difference in mass expressed in energy units represents the energy yield Q of the nuclear fusion reaction.

While the energy yield is very small compared to the masses of the nuclei involved in the fusion, it is nevertheless a very large energy yield. The nature of this energy is not specified by the above fusion reaction, but the fusion energy release can be analyzed by conservation of energy and momentum and one finds that the neutron carries 75% of the energy after the fusion.

Deuterium-Tritium Fusion

The most promising of the hydrogen fusion reactions which make up the deuterium cycle is the fusion of deuterium and tritium. The reaction yields 17.6 MeV of energy but to achieve fusion one must penetrate the coulomb barrier with the aid of tunneling, requiring very high temperatures . 80% of that energy yield is in the energy of the neutron, which is not as easily utilized as if it were carried by a charged particle. The deuterium fuel is abundant, but tritium must be either bred from lithium or gotten in the operation of the deuterium cycle. Compare with fission Conditions for fusion

Hydrogen Fusion Reactions

Even though a lot of energy is required to overcome the Coulomb barrier and initiate hydrogen fusion, the energy yields are enough to encourage continued research. Hydrogen fusion on the earth could make use of the reactions:

These reactions are more promising than the proton-proton fusion of the stars for potential energy sources. Of these the deuterium-tritium fusion appears to be the most promising and has been the subject of most experiments. In a deuterium-deuterium reactor, another reaction could also occur, creating a deuterium cycle:

Deuterium Cycle of Fusion

The four fusion reactions which can occur with deuterium can be considered to form a deuterium cycle. The four reactions:

can be combined as

or, omitting those constituents whose concentrations do not change:

Tritium Breeding

Deuterium-Tritium fusion is the most promising of the hydrogen fusion reactions, but no tritium occurs in nature since it has a 10 year half-life. The most promising source of tritium seems to be the breeding of tritium from lithium-6 by neutron bombardment with the reaction

which can be achieved by slow neutrons. This would occur if lithium were used as the coolant and heat transfer medium around the reaction chamber of a fusion reactor. Lithium-6 makes up 7.4% of natural lithium. While this constitutes a sizable supply, it is the limiting resource for the D-T process since the supply of deuterium fuel is virtually unlimited. With fast neutrons, tritium can be bred from the more abundant Li-7:

The conceptual sketch below is grossly oversimplified since the engineering for handling liquid lithium is quite complex.

Deuterium Source

Since the most practical nuclear fusion reaction for power generation seems to be the deuterium-tritium reaction, the sources of these fuels are important. The deuterium part of the fuel does not pose a great problem because about 1 part in 5000 of the hydrogen in seawater is deuterium. This amounts to over 10¹⁵ tons of deuterium. Viewed as a potential fuel for a fusion reactor, a gallon of seawater could produce as much energy as 300 gallons of gasoline. The tritium part of the fuel is more problematic - there is no sizable natural source since tritium is radioactive with a halflife of about 10 years. It would have to be obtained by breeding the tritium from lithium.

Fusion Energy Release

A large amount of energy is released by nuclear fusion reactions. It seems that for power generation, the deuterium-tritium reaction is the most practical, but it provides most of the energy to the released neutron. That is problematic because it is harder to extract the energy from neutrons compared to charged particles. The deuterium-deuterium fusion divides its output energy between neutrons and protons. The proton fraction interacts by the electromagnetic force with the medium and converts its kinetic energy to thermal energy very quickly.

It is practical to examine the kinetic energies of the products of nuclear fusion in the center of mass frame of reference. This amounts to neglecting the kinetic energies of the reacting particles before the fusion, which is justified by the fact that those energies are usually in the 1-10 keV range, and the fusion yield is in the MeV range. In the CM frame the energies of constituents a and b in terms of the fusion energy release Q are:

The magnitudes of the momenta in that frame are equal:

Combining these two equations gives:

This allows us to determine the relative magnitudes of the energies of the two fusion products:

For D-D fusion, the smaller particle carries 75% of the energy. With m(He3) = 2.8084 GeV/c2, m(H3) = 2.8089 GeV/c2,m(n) = 0.9396GeV/c2, and m(p) = 0.9383GeV/c2, the product energies for deuterium-deuterium fusion are shown. With a total yield of 3.27 MeV for the neutron reaction, the neutron carries 74.93% of the yield. For the proton reaction with yield 4.03 MeV, the proton carries 74.96%.

For D-T fusion, the smaller particle carries 80% of the energy. With m(He4) = 3.7274 GeV/c2 and m(n) = 0.9396 GeV/c2, the product energies for deuterium-tritium fusion are shown. With a total yield of 17.59 MeV for this reaction, the neutron carries 79.87% of the yield.