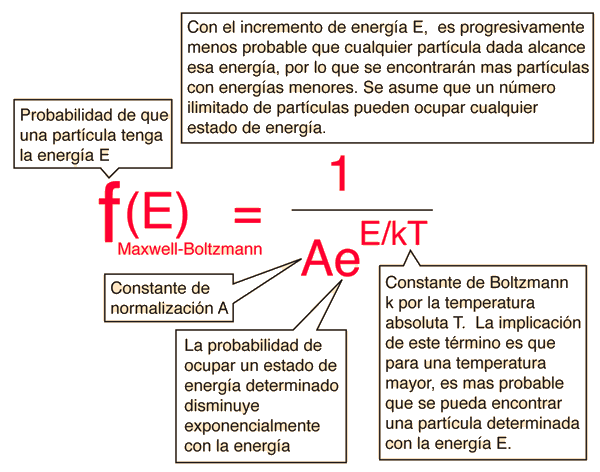
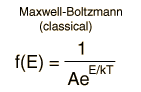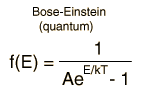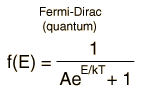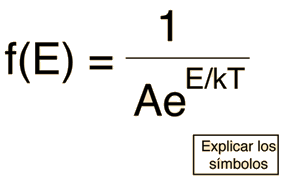La Distribución de Maxwell-Boltzmann
La distribución de Maxwell-Boltzmann es la función de distribución clásica, para la distribución de una cantidad de energía entre partículas idénticas pero distinguibles.
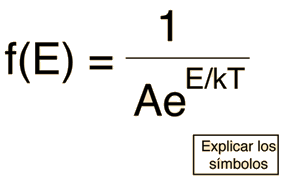
Además de la presunción de distinguibilidad, la física estadística clásica postula que:
- No hay ninguna restricción sobre el número de partículas que pueden ocupar un estado dado.
- En el equilibrio térmico, la distribución de partículas entre los estados de energía disponibles, se llevará a cabo con la distribución más probable, la cual es consistente con la energía total disponible y el número total de partículas.
- Cada estado específico del sistema tiene la misma probabilidad.
Una de las ideas generales contenidas en estos postulados, es que es poco probable que cualquier partícula consiga una energía muy por encima de la media (es decir, mucho más de lo que le corresponde). Las energías más bajas que la media, se ven favorecidas debido a que hay más maneras de conseguirlas. Si por ejemplo, una partícula tiene una energía de 10 veces el promedio, entonces, reduce el número de posibilidades para la distribución del resto de la energía. Por lo tanto, es poco probable ya que la probabilidad de ocupación de un estado dado, es proporcional al número de formas en que se puede conseguir.
|
Índice
Conceptos de Estadística Aplicada
Referencia
Blatt
Cap. 11. |