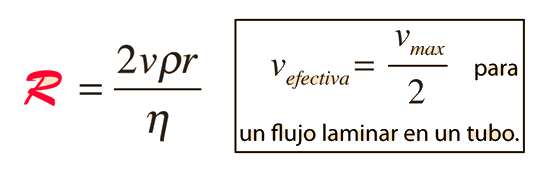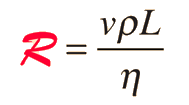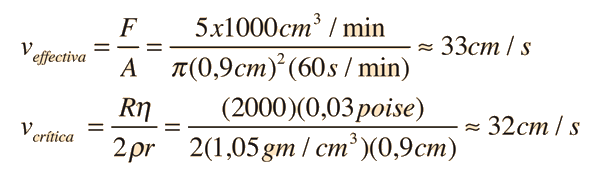Flujo Turbulento

La descripción de flujo tal como en la ley de Poiseuille, son válidas solamente para condiciones de flujo laminar. A una cierta velocidad crítica, el flujo se volverá turbulento, con la formación de remolinos y movimiento caótico que no contribuyen al caudal de volumen. Esta turbulencia aumenta la resistencia de manera espectacular. Para obtener un aumento del caudal, se necesitará un gran aumento en la presión. Estudios experimentales han caracterizado la velocidad crítica para el caso de un gran tubo largo recto, en la fórmula

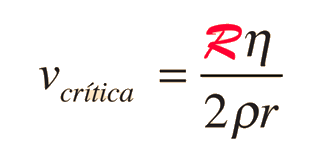
que depende de la viscosidad en poise, la densidad en gm/cm³, el radio del tubo en cm. El símbolo R es una constante experimental llamada el número de Reynold. El número de Reynolds reportado para el flujo de sangre es de aproximadamente 2000. De acuerdo con este criterio, el flujo sanguíneo modelado para la aorta humana, lleva a la expectativa de algunas turbulencias en el centro de la corriente.

Número de Reynolds

para el flujo a través de un tubo. Otro método consiste en definir una variable número de Reynolds, en función de la velocidad máxima de flujo laminar en un tubo por

y caracterizar el estado de turbulencia como la condición cuando el número de Reynolds alcanza un valor crítico como 2000. Para un enfoque más general a la turbulencia, cuando los objetos se mueven a través de un fluido, la relación tiene la siguiente forma:

donde L es una longitud característica asociada al objeto.

La turbulencia en el flujo no es algo que se pueda calcular con precisión, pero el concepto del número de Reynolds es de utilidad en la ingeniería general de los problemas de flujo de fluidos. Cuando las mediciones se realicen para una geometría particular y se establezca con ello un número de Reynolds experimental, este puede tener cierto poder predictivo y puede entonces ser útil en una ampliación del tamaño de esa geometría.

Referencias:

Encyclopedia of Science, Darling

Reynolds Number, NASA

¿Flujo Turbulento en la Aorta?

El flujo de sangre en el cuerpo humano esta muy libre de turbulencias, pero se pueden descubrir por estetoscopio asociados con la aorta, sonidos atribuidos a turbulencia. El modelo del flujo, hace uso del número de Reynold y la velocidad crítica asociada. Asumiendo un caudal de volumen de sangre nominal de 5 litros/min y un radio de 0,9 cm. para la aorta:

Sin embargo, cuando se tiene en cuenta el perfil de velocidad para el flujo del tubo, se encuentra que la velocidad máxima del flujo es el doble del valor efectivo, por lo que se esperaría una velocidad de 66 cm/s, para producir turbulencia en el centro de la aorta.

Fluido No Newtoniano